8235. Найдите двугранные углы трёхгранного угла, плоские углы которого равны 90^{\circ}
, 90^{\circ}
и \alpha
.
Ответ. 90^{\circ}
, 90^{\circ}
, \alpha
.
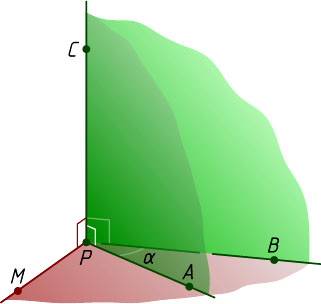
Решение. Рассмотрим трёхгранный угол PABC
с вершиной P
. Пусть \angle APC=\angle BPC=90^{\circ}
, \angle APB=\alpha
. Так как AP\perp CP
и BP\perp CP
, то APB
— линейный угол двугранного угла с ребром CP
. По условию задачи \angle APB=\alpha
.
В плоскости APB
проведём перпендикуляр PM
к прямой PB
. Тогда CPM
— линейный угол двугранного угла с ребром BP
. Прямая PC
перпендикулярна двум пересекающимся прямым AP
и BP
плоскости APB
, поэтому CP\perp MP
. Следовательно, \angle CPM=90^{\circ}
. Аналогично, линейный угол двугранного угла с ребром AP
также равен 90^{\circ}
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 2, с. 60
