8236. Все плоские углы трёхгранного угла равны 90^{\circ}
. Найдите углы между биссектрисами плоских углов.
Ответ. 60^{\circ}
.
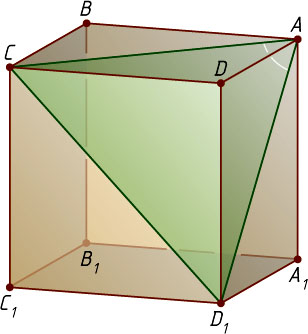
Решение. Рассмотрим куб ABCDA_{1}B_{1}C_{1}D_{1}
. Плоские углы трёхгранного угла ABDA_{1}
с вершиной A
равны 90^{\circ}
. Найдём угол между биссектрисой AC
плоского угла BAD
и биссектрисой AD_{1}
плоского угла DAA_{1}
. Для этого рассмотрим треугольник CAD_{1}
. Его стороны — диагонали равных квадратов. Значит, этот треугольник равносторонний. Следовательно, \angle CAD_{1}=60^{\circ}
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 3, с. 60
