8238. На какое наименьшее число непересекающихся трёхгранных углов можно разбить пространство?
Ответ. На четыре.
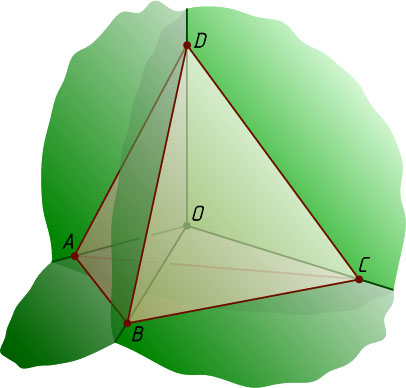
Решение. Пусть O
— точка внутри треугольной пирамиды ABCD
. Тогда четыре трёхгранных угла OABC
, OABD
, OACD
и OBCD
с общей вершиной O
удовлетворяют условию задачи.
Ясно, что пространство нельзя разбить два и на три непересекающихся трёхгранных угла.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 5, с. 60
