8241. Противоположные рёбра треугольной пирамиды попарно равны. Докажите, что все грани этой пирамиды — равные остроугольные треугольники.
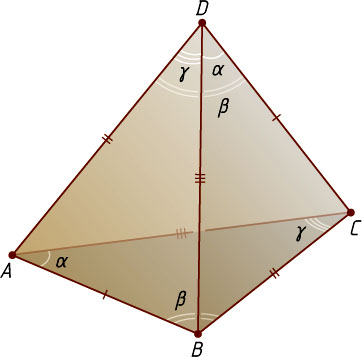
Решение. Рассмотрим треугольную пирамиду ABCD
, в которой AB=CD
, AD=BC
и AC=BD
. Треугольники ADB
, CBD
, DAC
и BCA
равны по трём сторонам. Значит, углы этих треугольников, лежащие против равных сторон, попарно равны. Обозначим
\angle ABD=\angle BDC=\angle ACD=\angle BAC=\alpha,
\angle BAD=\angle BCD=\angle ADC=\angle ABC=\beta.
\angle ADB=\angle CBD=\angle DAC=\angle BCA=\gamma,
Тогда плоские углы трёхгранного угла DABC
с вершиной D
равны \alpha
, \beta
и \gamma
.
Предположим, что \gamma\gt90^{\circ}
. Так как сумма двух плоских углов трёхгранного угла больше третьего плоского угла, то
\alpha+\beta\gt\gamma\gt90^{\circ}.
Тогда \alpha+\beta+\gamma\gt180^{\circ}
, что невозможно, так как сумма углов треугольника равна 180^{\circ}
. Аналогично, \alpha\lt90^{\circ}
и \beta\lt90^{\circ}
. Таким образом треугольники ADB
, CBD
, DAC
и BCA
— остроугольные.
Источник: Прасолов В. В., Шарыгин И. Ф. Задачи по стереометрии. — М.: Наука, 1989. — № 6.49, с. 106
Источник: Прасолов В. В. Задачи по стереометрии. — 2-е изд. — М.: МЦНМО, 2016. — № 8.59, с. 115
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 8, с. 61
