8245. Все плоские углы трёхгранного угла прямые. Докажите, что любое его сечение, не проходящее через вершину, есть остроугольный треугольник.
Решение. Пусть точки A
, B
и C
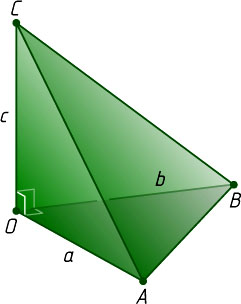
, отличные от точки O
, лежат на рёбрах данного трёхгранного угла с вершиной O
. Обозначим OA=a
, OB=b
, OC=c
. Из прямоугольных треугольников AOB
, AOC
и BOC
по теореме Пифагора находим, что
AB^{2}=a^{2}+b^{2},~AC^{2}=a^{2}+c^{2},~BC^{2}=b^{2}+c^{2}.
По теореме косинусов
\cos\angle BAC=\frac{AB^{2}+AC^{2}-BC^{2}}{2AB\cdot AC}=\frac{a^{2}+b^{2}+a^{2}+c^{2}-b^{2}-c^{2}}{2AB\cdot AC}=\frac{a^{2}}{AB\cdot AC}\gt0.
Следовательно, \angle BAC\lt90^{\circ}
. Аналогично, остальные углы треугольника ABC
также острые.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 16, с. 62
Источник: Понарин Я. П. Элементарная геометрия. — Т. 2: Стереометрия. — М.: МЦНМО, 2006. — № 3.13, с. 64
