8264. Сколько существует различных пирамид, все рёбра которых равны 1?
Ответ. Три.
Решение. Рассмотрим n
-гранный угол при вершине правильной n
-угольной пирамиды, все рёбра которой равны 1. Боковые грани такой пирамиды — равносторонние треугольники со стороной 1. Поэтому все плоские углы рассматриваемого n
-гранного угла равны 60^{\circ}
. Так как сумма плоских углов выпуклого многогранного угла меньше 360^{\circ}
, то 60^{\circ}\cdot n\lt360^{\circ}
. Значит, n\lt6
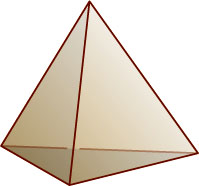
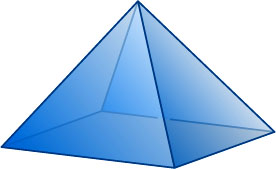
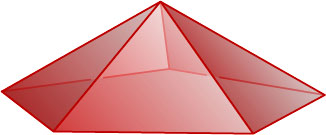
. Таким образом, условию задачи могут удовлетворять только три пирамиды: треугольная (правильный тетраэдр), четырёхугольная и пятиугольная. Можно построить четырёхугольную и пятиугольную пирамиду, все рёбра которых равны 1.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 4, с. 66


