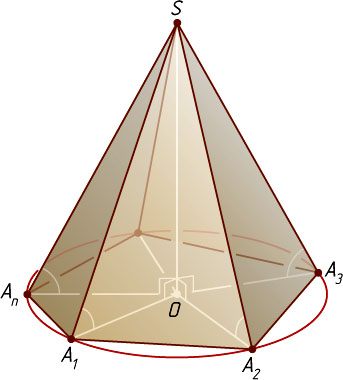
8265. Докажите, что если боковые рёбра пирамиды образуют с плоскостью основания равные углы, то в основании лежит вписанный многоугольник, а высота пирамиды проходит через центр описанной окружности этого многоугольника.
Решение. Пусть SO
— высота данной пирамиды SA_{1}A_{2}\dots A_{n}
с вершиной S
. Тогда SA_{1}O
, SA_{2}O
, \dots
, SA_{n}O
— углы боковых рёбер пирамиды с плоскостью основания A_{1}A_{2}\dots A_{n}
. По условию задачи
\angle SA_{1}O=\angle SA_{2}O=\dots=\angle SA_{n}O,
поэтому прямоугольные треугольники SA_{1}O
, SA_{2}O
, \dots
, SA_{n}O
равны по катету (SO
— общий катет) и противолежащему острому углу. Значит,
OA_{1}=OA_{2}=\dots=OA_{n}.
Следовательно, точка O
равноудалена от всех вершин многоугольника A_{1}A_{2}\dots A_{n}
, т. е. O
— центр окружности, описанной около многоугольника A_{1}A_{2}\dots A_{n}
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 5, с. 66
