8266. В основании треугольной пирамиды лежит прямоугольный треугольник с катетами a
и b
. Боковые рёбра равны l
. Найдите высоту пирамиды.
Ответ. \frac{1}{2}\sqrt{4l^{2}-a^{2}-b^{2}}
.
Указание. Поскольку боковые рёбра пирамиды равны, её высота проходит через центр окружности, описанной около основания.
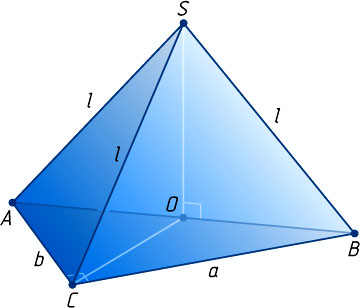
Решение. Пусть SABC
— данная пирамида. Поскольку её боковые рёбра равны, высота SO
проходит через центр O
окружности, описанной около основания, а так как основание пирамиды — прямоугольный треугольник ABC
, то O
— середина его гипотенузы AB
, а радиус описанной окружности треугольника равен половине гипотенузы, т. е.
R=\frac{1}{2}\sqrt{a^{2}+b^{2}}.
Из прямоугольного треугольника AOS
по теореме Пифагора находим, что
SO=\sqrt{SA^{2}-OA^{2}}=\sqrt{l^{2}-\frac{1}{4}(a^{2}+b^{2})}=\frac{1}{2}\sqrt{4l^{2}-a^{2}-b^{2}}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 6, с. 66
