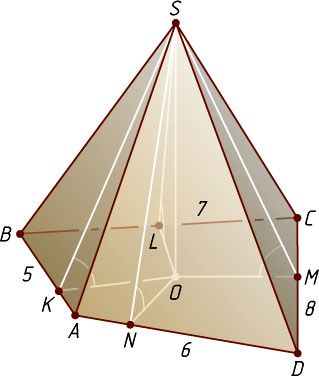
8268. Три последовательные стороны основания четырёхугольной пирамиды равны 5, 7 и 8. Найдите четвёртую сторону основания, если известно, что двугранные углы при основании равны.
Ответ. 6.
Указание. Докажите, что в основание данной пирамиды можно вписать окружность.
Решение. Пусть SO
— высота пирамиды SABCD
, в которой AB=5
, BC=7
, CD=8
и боковые грани образуют равные углы с плоскостью основания. Опустим перпендикуляры OK
, OL
, OM
и ON
из точки O
на прямые AB
, BC
, CD
и AD
соответственно. По теореме о трёх перпендикулярах SK\perp AB
, SL\perp BC
, SM\perp CD
и SN\perp AD
. Поэтому OKS
, OLS
, OMS
и ONS
— линейные углы двугранных углов при соответствующих сторонах основания пирамиды.
По условию задачи
\angle OKS=\angle OLS=\angle OMS=\angle ONS.
Значит, прямоугольные треугольники OKS
, OLS
, OMS
и ONS
равны по катету и противолежащему острому углу. Поэтому OK=OL=OM=ON
, т. е. точка O
равноудалена от прямых AB
, BC
, CD
и AD
. Следовательно, O
— центр окружности, вписанной в четырёхугольник ABCD
. По свойству описанного четырёхугольника AB+CD=BC+AD
, откуда
AD=AB+CD-BC=5+8-7=6.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 8, с. 67
