8269. В пирамиде ABCD
площадь грани ABC
в четыре раза больше площади грани ABD
. На ребре CD
взята точка M
, причём CM:MD=2
. Через точку M
проведены плоскости, параллельные граням ABC
и ABD
. Найдите отношение площадей получившихся сечений.
Ответ. 1
.
Решение. Обозначим S_{\triangle ABD}=S
. Тогда S_{\triangle ABC}=4S
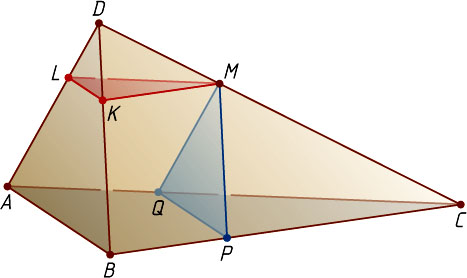
. Пусть плоскость, проходящая через точку M
параллельно плоскости ABC
, пересекает рёбра AD
и BD
соответственно в точках L
и K
, а плоскость, проходящая через точку M
параллельно плоскости ABD
, пересекает рёбра BC
и AC
соответственно в точках P
и Q
. Тогда треугольник LKM
подобен треугольнику ABC
с коэффициентом \frac{DM}{DC}=\frac{1}{3}
, а треугольник QPM
подобен треугольнику ABD
с коэффициентом \frac{CM}{CD}=\frac{2}{3}
. Поэтому
S_{\triangle LKM}=\left(\frac{1}{3}\right)^{2}S_{\triangle ABC}=\frac{1}{9}\cdot4S=\frac{4}{9}S,~S_{\triangle QPM}=\left(\frac{2}{3}\right)^{2}\cdot S_{\triangle ABD}=\frac{4}{9}S.
Следовательно,
\frac{S_{\triangle LKM}}{S_{\triangle QPM}}=\frac{\frac{4}{9}S}{\frac{4}{9}S}=1.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 9, с. 67
