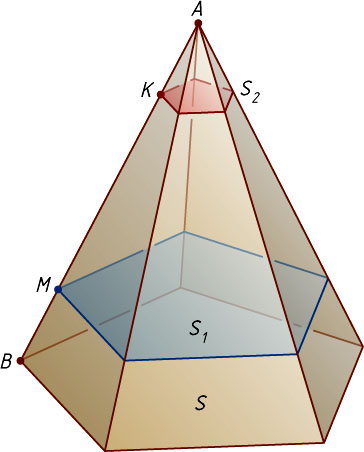
8271. На боковом ребре AB
пирамиды взяты точки K
и M
, причём AK=BM
. Через эти точки проведены сечения, параллельные основанию пирамиды. Известно, что сумма площадей этих сечений составляет \frac{2}{3}
площади основания пирамиды. Найдите отношение KM:AB
.
Ответ. \frac{\sqrt{3}}{3}
.
Решение. Пусть S
— площадь основания пирамиды, S_{1}
и S_{2}
— площади сечений, проведённых через точки K
и M
соответственно. Эти сечения есть многоугольники, подобные многоугольнику основания пирамиды с коэффициентами \frac{AK}{AB}
и \frac{AM}{AB}
соответственно. Обозначим KM=x
, AB=y
. Тогда
AK=BM=\frac{y-x}{2},~AM=AK+KM=\frac{y-x}{2}+x=\frac{y+x}{2},
S_{1}=\left(\frac{AK}{AB}\right)^{2}\cdot S=\left(\frac{y-x}{2y}\right)^{2}\cdot S,~S_{2}=\left(\frac{AM}{AB}\right)^{2}\cdot S=\left(\frac{y+x}{2y}\right)^{2}\cdot S.
Так как S_{1}+S_{2}=\frac{2}{3}S
, то
\left(\frac{y-x}{2y}\right)^{2}\cdot S+\left(\frac{y+x}{2y}\right)^{2}\cdot S=\frac{2}{3}S,~\left(\frac{y-x}{2y}\right)^{2}+\left(\frac{y+x}{2y}\right)^{2}=\frac{2}{3},
откуда находим, что
\frac{KM}{AB}=\frac{y}{x}=\frac{\sqrt{3}}{3}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 11, с. 67
