8272. Все двугранные углы при основании пирамиды равны \alpha
, а углы, образуемые боковыми рёбрами с плоскостью основания, равны \beta
. Известно, что \tg\alpha=k\tg\beta
. Сколько сторон имеет основание пирамиды, если k=2
? Какие значения может принимать величина k
?
Ответ. n=3
; k=\frac{1}{\cos\frac{180^{\circ}}{n}}
, где n=3
, 4, ….
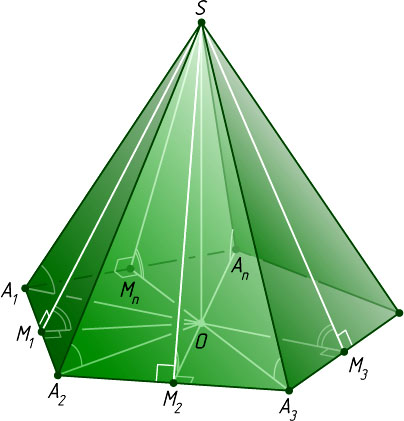
Решение. Пусть SO
— высота данной пирамиды SA_{1}A_{2}\dots A_{n}
с вершиной S
, Из условия задачи следует, что SA_{1}=SA_{2}=\dots=SA_{n}
. Значит,
OA_{1}=OA_{2}=\dots=OA_{n}.
Медианы SM_{1}
, SM_{2}
, \dots
, SM_{n}
равнобедренных треугольников SA_{1}A_{2}
, SA_{2}A_{3}
, \dots
, SA_{n}A_{1}
являются высотами. Медианы OM_{1}
, OM_{2}
, \dots
, OM_{n}
равнобедренных треугольников A_{1}OA_{2}
, A_{2}OA_{3}
, \dots
, A_{n}OA_{1}
также являются высотами. Поэтому SM_{1}O
, SM_{2}O
, \dots
, SM_{n}O
— линейные углы двугранных углов при основании пирамиды. По условию задачи
\angle SM_{1}O=\angle SM_{2}O=\dots=\angle SM_{n}O,
поэтому прямоугольные треугольники SM_{1}O
, SM_{2}O
, \dots
, SM_{n}O
равны по катету (SO
— общий катет) и острому углу. Значит,
OM_{1}=OM_{2}=\dots=OM_{n}.
Следовательно, равнобедренные треугольники A_{1}OA_{2}
, A_{2}OA_{3}
, \dots
, A_{n}OA_{1}
равны (по боковым сторонам и высотам, опущенным на основания). Поэтому все стороны и все углы многоугольника A_{1}A_{2}\dots A_{n}
равны. Значит, этот многоугольник правильный, а высота SO
пирамиды проходит через его центр O
. Следовательно, пирамида SA_{1}A_{2}\dots A_{n}
— правильная.
Пусть
OM_{1}=OM_{2}=\dots=OM_{n}=r,~OA_{1}=OA_{2}=\dots=OA_{n}=R
(r
и R
— радиусы вписанной и описанной окружностей правильного многоугольника A_{1}A_{2}\dots A_{n}
). Тогда
r=\frac{SO}{\tg\alpha},~R=\frac{SO}{\tg\beta}.
Обозначим через \varphi
угол правильного многоугольника A_{1}A_{2}\dots A_{n}
. Тогда
\varphi=\frac{180^{\circ}(n-2)}{n},~\frac{\varphi}{2}=90^{\circ}-\frac{180^{\circ}}{n},~\cos\frac{180^{\circ}}{n}=\sin\frac{\varphi}{2}=\frac{r}{R}=\frac{\tg\beta}{\tg\alpha}=\frac{1}{k}.
Если k=2
, то
\sin\frac{\varphi}{2}=\frac{1}{2},~\frac{\varphi}{2}=30^{\circ},~\varphi=60^{\circ}.
В этом случае n=3
.
Из равенства \cos\frac{180^{\circ}}{n}=\frac{1}{k}
следует, что число k
может принимать любые значения вида \frac{1}{\cos\frac{180^{\circ}}{n}}
, где n=3
, 4, ….
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 12, с. 67
