8273. В основании треугольной пирамиды лежит правильный треугольник. Высота пирамиды равна h
. Все боковые грани наклонены к плоскости основания под углом \alpha
. Найдите площадь основания. (Укажите все возможности.)
Ответ. 3h^{2}\sqrt{3}\ctg^{2}\alpha
; \frac{1}{3}h^{2}\sqrt{3}\ctg^{2}\alpha
.
Решение. Поскольку боковые грани пирамиды образуют равные двугранные углы с плоскостью основания, высота пирамиды проходит либо через центр вписанной, либо через центр одной из вневписанных окружностей треугольника основания.
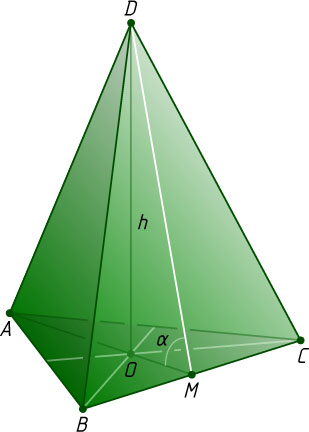
Пусть высота пирамиды проходит через центр O
вписанной окружности основания ABC
треугольной пирамиды ABCD
, M
— середина BC
(рис. 1). Обозначим AB=BC=AC=a
. Так как OM\perp BC
, то по теореме о трёх перпендикулярах DM\perp BC
, поэтому DMO
— линейный угол двугранного угла образованного боковой гранью DBC
с плоскостью основания ABC
. По условию задачи \angle DMO=\alpha
, DO=h
. Из прямоугольного треугольника DMO
находим, что
OM=DO\ctg\angle DMO=h\ctg\alpha.
С другой стороны, так как OM
— радиус вписанной окружности равностороннего треугольника со стороной a
, то OM=\frac{a\sqrt{3}}{6}
. Из уравнения \frac{a\sqrt{3}}{6}=h\ctg\alpha
находим, что a=2h\sqrt{3}\ctg\alpha
. Следовательно,
S_{\triangle ABC}=\frac{a^{2}\sqrt{3}}{4}=(2h\sqrt{3}\ctg\alpha)^{2}\cdot\frac{\sqrt{3}}{4}=3h^{2}\sqrt{3}\ctg^{2}\alpha.
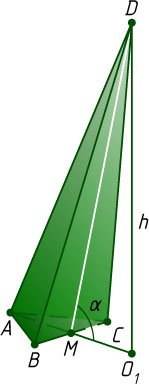
Пусть высота пирамиды проходит через центр O_{1}
вневписанной окружности, касающейся стороны BC
основания ABC
пирамиды ABCD
(рис. 2). Аналогично предыдущему находим, что
O_{1}M=DO\ctg\angle DMO=h\ctg\alpha.
С другой стороны, так как O_{1}M
— радиус вневписанной окружности равностороннего треугольника со стороной a
, то O_{1}M=\frac{a\sqrt{3}}{2}
. Из уравнения \frac{a\sqrt{3}}{2}=h\ctg\alpha
находим, что a=\frac{2}{3}h\sqrt{3}\ctg\alpha
. Следовательно,
S_{\triangle ABC}=\frac{a^{2}\sqrt{3}}{4}=\left(\frac{2}{3}h\sqrt{3}\ctg\alpha\right)^{2}\cdot\frac{\sqrt{3}}{4}=\frac{1}{3}h^{2}\sqrt{3}\ctg^{2}\alpha.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 14, с. 67

