8275. Сторона основания правильной треугольной пирамиды равна a
, боковое ребро равно b
. Найдите высоту пирамиды и двугранный угол между боковыми гранями.
Ответ. \frac{\sqrt{3b^{2}-a^{2}}}{\sqrt{3}}
, 2\arctg\frac{b}{\sqrt{3b^{2}-a^{2}}}
.
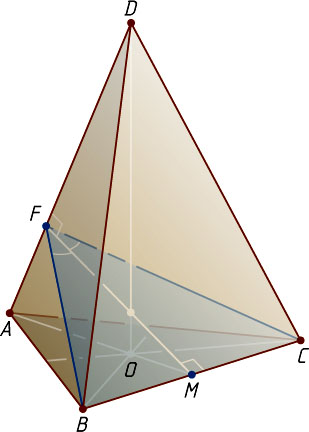
Решение. Пусть O
— центр основания ABC
правильной треугольной пирамиды ABCD
, M
— середина BC
, F
— основание перпендикуляра, опущенного из точки M
на боковое ребро AD
, AB=BC=AC=a
, AD=BD=CD=b
. Из прямоугольного треугольника DAO
находим, что
DO=\sqrt{AD^{2}-AO^{2}}=\sqrt{b^{2}-\left(\frac{a\sqrt{3}}{3}\right)^{2}}=\frac{\sqrt{3b^{2}-a^{2}}}{\sqrt{3}},
\sin\angle DAO=\frac{DO}{AD}=\frac{\sqrt{3b^{2}-a^{2}}}{b\sqrt{3}}.
Прямая AM
— ортогональная проекция наклонной AD
на плоскость ABC
. Так как AM\perp BC
, то по теореме о трёх перпендикулярах AD\perp BC
. Значит, прямая AD
перпендикулярна двум пересекающимся прямым MF
(по построению) и BC
. Следовательно, BFC
— линейный угол двугранного угла между плоскостями боковых граней ADB
и ADC
.
Из прямоугольных треугольников AFM
и BMF
находим, что
MF=AM\sin\angle DAO=\frac{a\sqrt{3}}{2}\cdot\frac{\sqrt{3b^{2}-a^{2}}}{b\sqrt{3}}=\frac{a\sqrt{3b^{2}-a^{2}}}{2b},
\tg\frac{1}{2}\angle BFC=\frac{BM}{MF}=\frac{\frac{1}{2}a}{\frac{a\sqrt{3b^{2}-a^{2}}}{2b}}=\frac{b}{\sqrt{3b^{2}-a^{2}}}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 16, с. 68
