8276. На гранях правильного тетраэдра с ребром a
как на основаниях построены правильные тетраэдры. Докажите, что новые вершины построенных тетраэдров являются вершинами правильного тетраэдра. Найдите его ребро.
Ответ. \frac{5a}{3}
.
Решение. Пусть ABCD
— правильный тетраэдр с ребром a
; D_{1}
, A_{1}
, B_{1}
и C_{1}
— центры его граней ABC
, DBC
, ACD
и ABD
соответственно; D_{2}
, A_{2}
, B_{2}
и C_{2}
— вершины правильных тетраэдров D_{2}ABC
, A_{2}BCD
, B_{2}ACD
и C_{2}BAD
.
Отрезки DD_{1}
и D_{2}D_{1}
— высоты правильных тетраэдров с общей гранью ABC
. Поэтому точки D
, D_{1}
и D_{2}
лежат на одной прямой, причём D_{1}
— середина DD_{2}
. Аналогично, A_{1}
— середина отрезка AA_{2}
. Прямые AA_{1}
и DD_{1}
лежат в плоскости AMD
, где M
— середина BC
, причём \frac{MA_{1}}{DM}=\frac{MD_{1}}{AM}=\frac{1}{3}
, так как A_{1}
и D_{1}
— точки пересечения медиан треугольников BCD
и ABC
. Поэтому
A_{1}D_{1}\parallel AD,~A_{1}D_{1}=\frac{1}{3}AD.
Кроме того, точки A_{1}
и D_{1}
— середины диагоналей AA_{2}
и DD_{2}
трапеции ADA_{2}D_{2}
. Значит,
A_{1}D_{1}=\frac{1}{2}(A_{2}D_{2}-AD),
откуда находим, что
A_{2}D_{2}=2A_{1}D_{1}+AD=\frac{2}{3}a+a=\frac{5}{3}a.
Аналогично находим, что остальные рёбра треугольной пирамиды A_{2}B_{2}C_{2}D_{2}
равны \frac{5}{3}a
.
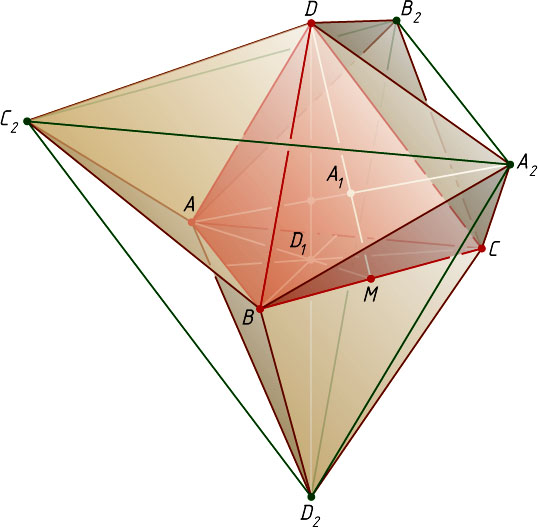
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 17, с. 68
