8277. На гранях правильного тетраэдра с ребром a
как на основаниях построены равные правильные пирамиды. Плоские углы в этих пирамидах при вершинах, противолежащих граням тетраэдра, прямые. Рассмотрим многогранник, образованный тетраэдром и построенными пирамидами. Сколько граней у этого многогранника? Как он называется?
Ответ. 6 граней; куб.
Указание. Достройте правильный тетраэдр до параллелепипеда, проведя через его противоположные рёбра три пары параллельных плоскостей.
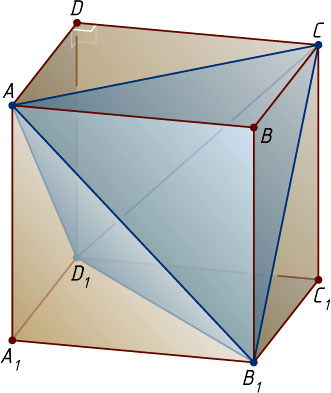
Решение. Рассмотрим куб ABCDA_{1}B_{1}C_{1}D_{1}
. Все рёбра треугольной пирамиды ACB_{1}D_{1}
равны. Значит, эта пирамида — правильный тетраэдр. На боковых гранях правильного тетраэдра ACB_{1}D_{1}
как на основаниях построены правильные треугольные пирамиды DACD_{1}
с вершиной D
, A_{1}AB_{1}D_{1}
с вершиной A_{1}
, BAB_{1}C
с вершиной B
и C_{1}CB_{1}D_{1}
с вершиной C_{1}
. Плоские углы при вершинах этих четырёх пирамид равны по 90^{\circ}
.
Обратно, для любого правильного тетраэдра существует единственный куб, скрещивающиеся диагонали противоположных граней которого являются рёбрами данного правильного тетраэдра (достаточно провести через скрещивающиеся диагонали противоположных граней тетраэдра три пары параллельных плоскостей). На боковой грани этого тетраэдра как на основании можно построить внешним образом единственную правильную треугольную пирамиду, плоские углы при вершине которой прямые. Ясно, что боковые грани такой пирамиды лежат в гранях куба.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 18, с. 68
