8299. Три отрезка, не лежащие в одной плоскости, имеют общую точку и делятся этой точкой пополам. Докажите, что концы этих отрезков служат вершинами параллелепипеда.
Решение. Пусть O
— общая середина отрезков AA_{1}
, BB_{1}
и DD_{1}
. Тогда AB\parallel A_{1}B_{1}
и AD\parallel A_{1}D_{1}
. Значит, плоскости ABD
и A_{1}B_{1}D_{1}
параллельны. Аналогично, плоскость ADB_{1}
параллельна плоскости A_{1}D_{1}B
.
В плоскостях ABD
и A_{1}B_{1}D_{1}
возьмём соответственно точки C
и C_{1}
так, что ABCD
и A_{1}B_{1}C_{1}D_{1}
— параллелограммы. Так как CD\parallel AB
, AB\parallel A_{1}B_{1}
и A_{1}B_{1}\parallel C_{1}D_{1}
, то CD\parallel C_{1}D_{1}
. Поэтому плоскости ABD_{1}
и DB_{1}A_{1}
также параллельны. Шестигранник ABCDC_{1}D_{1}A_{1}B_{1}
, образован пересечением трёх пар параллельных плоскостей. Следовательно, это параллелепипед.
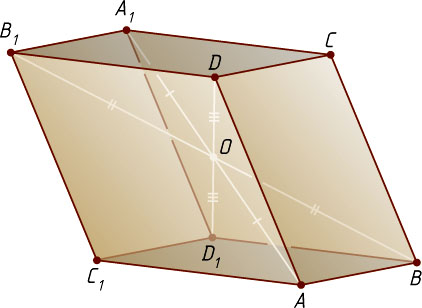
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 5, с. 73
