8301. Пусть V
— объём тетраэдра, S_{1}
и S_{2}
— площади двух граней, a
— длина их общего ребра, \varphi
— величина двугранного угла между ними. Докажите, что V=\frac{2}{3}\cdot\frac{S_{1}S_{2}\cdot\sin\varphi}{a}
.
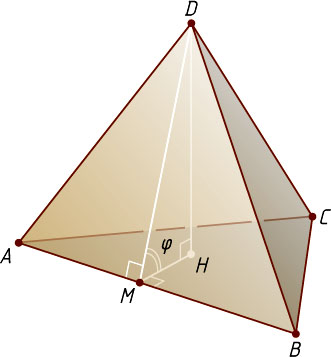
Решение. Пусть ребро AB
тетраэдра ABCD
равно a
, угол между гранями ABC
и ABD
равен \varphi
, S_{\triangle ABC}=S_{1}
, S_{\triangle ABD}=S_{2}
.
Если DH
— высота тетраэдра, опущенная на основание ABC
, а HM
— перпендикуляр, опущенный из точки H
на AB
, то по теореме о трёх перпендикулярах DM\perp AB
, значит, DMH
— линейный угол двугранного угла тетраэдра при ребре AB
. Поэтому \angle DMH=\varphi
. Тогда
V=V_{ABCD}=\frac{1}{3}S_{\triangle ABC}\cdot DH=\frac{1}{3}S_{1}\cdot DM\sin\varphi=
=\frac{1}{3}S_{1}\cdot\frac{2S_{2}}{a}\cdot\sin\varphi=\frac{2}{3}\cdot\frac{S_{1}S_{2}\cdot\sin\varphi}{a}.
Источник: Шарыгин И. Ф. Геометрия. Стереометрия: Задачник для 10—11 кл. — М.: Дрофа, 1998. — № 28, с. 7
Источник: Прасолов В. В., Шарыгин И. Ф. Задачи по стереометрии. — М.: Наука, 1989. — № 3.3, с. 45
Источник: Прасолов В. В. Задачи по стереометрии. — 2-е изд. — М.: МЦНМО, 2016. — № 3.3, с. 34
Источник: Понарин Я. П. Элементарная геометрия. — Т. 2: Стереометрия. — М.: МЦНМО, 2006. — с. 97
