8303. Рёбра прямоугольного параллелепипеда равны 2, 3 и 4. Найдите угол между его диагоналями.
Ответ. 2\arctg\frac{3\sqrt{5}}{10}=\arccos\frac{11}{29}
; 2\arctg\frac{2}{5}
; 2\arctg\frac{\sqrt{13}}{5}
.
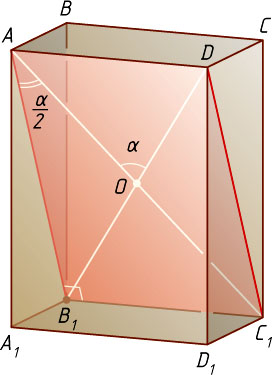
Решение. Рассмотрим прямоугольный параллелепипед ABCDA_{1}B_{1}C_{1}D_{1}
, в котором AB=2
, AD=3
, AA_{1}=4
. Пусть его диагонали пересекаются в точке O
. Сечение параллелепипеда плоскостью ADC_{1}B_{1}
— прямоугольник со сторонами
AD=B_{1}C_{1}=3,~DC_{1}=AB_{1}=\sqrt{AA_{1}+A_{1}B_{1}}=\sqrt{16+4}=2\sqrt{5}.
Обозначим \angle AOD=\alpha
. Угол AOD
— внешний угол равнобедренного треугольника AOB_{1}
, поэтому \angle C_{1}AB_{1}=\frac{\alpha}{2}
. Из прямоугольного треугольника AC_{1}B_{1}
находим, что
\tg\frac{\alpha}{2}=\frac{B_{1}C_{1}}{AB_{1}}=\frac{3}{2\sqrt{5}}=\frac{3\sqrt{5}}{10}\lt1.
Значит, \frac{\alpha}{2}\lt45^{\circ}
, а \alpha\lt90^{\circ}
. Поэтому AOD
— угол между диагоналями данного прямоугольного параллелепипеда. Так как \tg\frac{\alpha}{2}=\frac{3\sqrt{5}}{10}
, то
\cos\alpha=\frac{1-\tg^{2}\frac{\alpha}{2}}{1+\tg^{2}\frac{\alpha}{2}}=\frac{1-\frac{9}{20}}{1+\frac{9}{20}}=\frac{11}{29}.
Аналогично находим угол между диагоналями AC_{1}
и BD_{1}
, а также угол между диагоналями AC_{1}
и CA_{1}
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 7, с. 73
