8304. Ортогональные проекции отрезка на три попарно перпендикулярные прямые равны 1, 2 и 3. Найдите длину этого отрезка.
Ответ. \sqrt{14}
.
Решение. Пусть OM
— данный отрезок. Через точку O
проведём прямые a
, b
и c
, соответственно параллельные трём данным попарно перпендикулярным прямым. Тогда ортогональные проекции отрезка OM
на прямые a
, b
и c
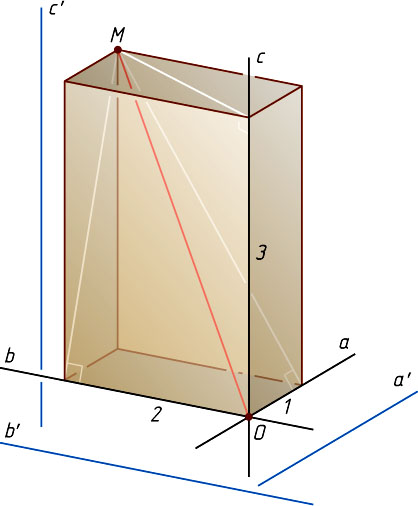
также равны 1, 2 и 3, а отрезок OM
есть диагональ прямоугольного параллелепипеда с измерениями 1, 2 и 3. Следовательно,
OM=\sqrt{1^{2}+2^{2}+3^{2}}=\sqrt{14}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 8, с. 73
