8305. Найдите расстояние между серединами непараллельных сторон разных оснований правильной треугольной призмы, все рёбра которой равны 2.
Ответ. \sqrt{5}
.
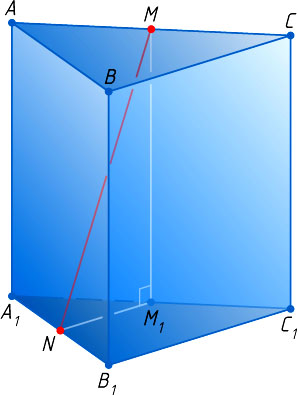
Решение. Пусть M
и N
— середины рёбер AC
и A_{1}B_{1}
правильной треугольной призмы ABCA_{1}B_{1}C_{1}
с основаниями ABC
и A_{1}B_{1}C_{1}
(AA_{1}\parallel BB_{1}\parallel CC_{1}
), все рёбра которой равны 2
; M_{1}
— ортогональная проекция точки M
на плоскость A_{1}B_{1}C_{1}
. Тогда M_{1}
— середина A_{1}C_{1}
, M_{1}N
— средняя линия треугольника A_{1}B_{1}C_{1}
. Из прямоугольного треугольника MM_{1}N
находим, что
MN=\sqrt{MM_{1}^{2}+NM_{1}^{2}}=\sqrt{4+1}=\sqrt{5}.
Ясно, что расстояния между серединами любых других непараллельных сторон основания также равны \sqrt{5}
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 9, с. 73
