8306. Покажите, что в кубе можно выбрать четыре вершины, являющиеся вершинами правильного тетраэдра, причём сделать это можно двумя способами.
Решение. Рассмотрим куб ABCDA_{1}B_{1}C_{1}D_{1}
(AA_{1}\parallel BB_{1}\parallel CC_{1}\parallel DD_{1}
) с ребром a
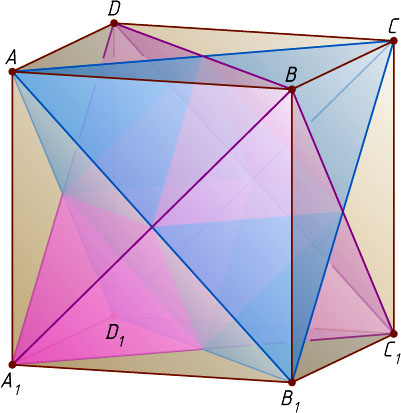
. Все рёбра пирамид ACB_{1}D_{1}
и BDA_{1}C_{1}
равны a\sqrt{2}
, поэтому эти пирамиды являются правильными тетраэдрами.
Докажем, что никакая другая четвёрка вершин куба не может образовать правильный тетраэдр. В самом деле, три вершины, принадлежащие одной грани куба не могут быть вершинами правильного тетраэдра, так как треугольник с вершинами в этих точках — прямоугольный. Остаётся случай, когда две вершины лежат в одной грани куба, а две другие — в противоположной. Если это, например, AB
и B_{1}C
, то AB\ne AC_{1}
, а если AB
и B_{1}D_{1}
, то AB\ne B_{1}D_{1}
. Остальное аналогично. Таким образом, возможны только случаи, когда две вершины тетраэдра являются концами диагонали грани куба, а две другие — концами скрещивающейся с ней диагонали противоположной грани.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 10, с. 73
