8307. Возможно ли, чтобы каждая вершина одного из двух тетраэдров принадлежала плоскости грани другого, и наоборот?
Ответ. Да.
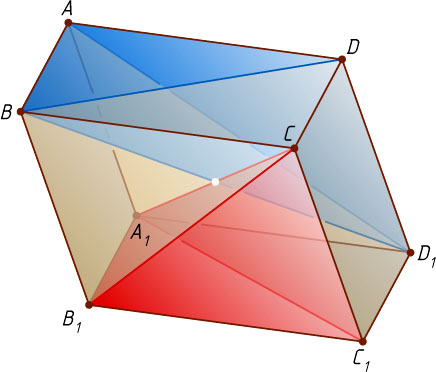
Решение. Рассмотрим параллелепипед ABCDA_{1}B_{1}C_{1}D_{1}
. Тетраэдры ABDD_{1}
и A_{1}B_{1}C_{1}C
удовлетворяют условию задачи. Действительно, вершины первого тетраэдра лежат в плоскостях граней второго:
вершина A
— в плоскости A_{1}C_{1}C
,
вершина B
— в плоскости B_{1}C_{1}C
,
вершина D
— в плоскости A_{1}B_{1}C
,
вершина D_{1}
— в плоскости A_{1}B_{1}C_{1}
;
вершины второго тетраэдра лежат в плоскостях граней первого:
вершина A_{1}
— в плоскости ADD_{1}
,
вершина B_{1}
— в плоскости BDD_{1}
,
вершина C_{1}
— в плоскости ABD_{1}
,
вершина C
— в плоскости ABD
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 11, с. 73
