8308. Через точку на ребре треугольной пирамиды проведены две плоскости, параллельные двум граням пирамиды. Эти плоскости отсекают две треугольные пирамиды. Разрежьте оставшийся многогранник на две треугольные призмы.
Решение. Пусть точка K
лежит на ребре AD
треугольной пирамиды ABCD
, плоскость, проведённая через точку K
параллельно плоскости ABC
, пересекает рёбра BD
и CD
соответственно в точках L
и M
, а плоскость, проведённая через точку K
параллельно плоскости BCD
пересекает рёбра AB
и AC
соответственно в точках P
и Q
.
Через точку Q
проведём прямую, параллельную AB
, до пересечения с ребром BC
в точке F
. Тогда
QF\parallel AB\parallel KL,~QF=AB\cdot\frac{CQ}{AC}=AB\cdot\frac{DK}{AD}=KL.
Поэтому KLFQ
— параллелограмм, а так как CMLF
и CMKQ
— также параллелограммы, то KLMQFC
— треугольная призма с основаниями KLM
и QFC
. Аналогично, KPQLBF
— треугольная призма с основаниями KPQ
и LBF
.
Таким образом, многогранник BCQPKLM
можно разрезать на треугольные призмы KLMQFC
и KPQLBF
.
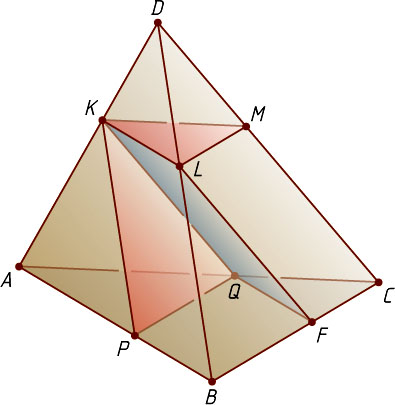
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 12, с. 73
