8310. Диагональ прямоугольного параллелепипеда образует с его рёбрами углы \alpha
, \beta
и \gamma
. Докажите, что \cos^{2}\alpha+\cos^{2}\beta+\cos^{2}\gamma=1
.
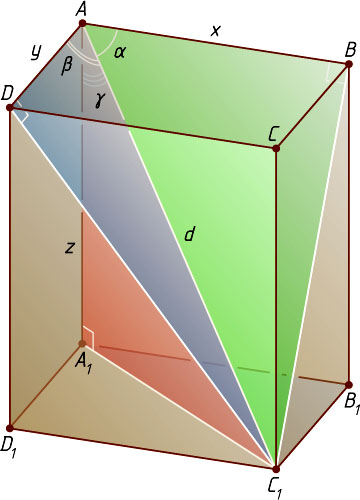
Решение. Пусть диагональ AC_{1}
образует с рёбрами AB
, AD
и AA_{1}
прямоугольного параллелепипеда ABCDA_{1}B_{1}C_{1}D_{1}
(AA_{1}\parallel BB_{1}\parallel CC_{1}\parallel DD_{1}
) углы \alpha
, \beta
и \gamma
соответственно. Обозначим
AB=x,~AD=y,~AA_{1}=z,~AC_{1}=d.
Из прямоугольных треугольников ABC_{1}
, ADC_{1}
и AA_{1}C_{1}
находим, что
\cos\alpha=\cos\angle BAC_{1}=\frac{AB}{AC_{1}}=\frac{x}{d},
\cos\beta=\cos\angle DAC_{1}=\frac{AD}{AC_{1}}=\frac{y}{d},
\cos\gamma=\cos\angle A_{1}AC_{1}=\frac{AA_{1}}{AC_{1}}=\frac{z}{d}.
Следовательно,
\cos^{2}\alpha+\cos^{2}\beta+\cos^{2}\gamma=\left(\frac{x}{d}\right)^{2}+\left(\frac{y}{d}\right)^{2}+\left(\frac{z}{d}\right)^{2}=
=\frac{x^{2}+y^{2}+z^{2}}{d^{2}}=\frac{d^{2}}{d^{2}}=1.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 14, с. 74
