8311. Каким может быть ребро куба, одна грань которого лежит в плоскости основания правильной четырёхугольной пирамиды, а четыре оставшиеся вершины — на её боковой поверхности, если стороны основания пирамиды равны a
, а высота пирамиды равна h
.
Ответ. \frac{ah}{a+h\sqrt{2}}\leqslant x\leqslant\frac{ah}{a+h}
.
Решение. Пусть вершины A
, B
, C
и D
куба ABCDA_{1}B_{1}C_{1}D_{1}
с ребром x
лежат на основании KLMN
правильной четырёхугольной пирамиды KLMNP
с вершиной P
, а вершины A_{1}
, B_{1}
, C_{1}
и D_{1}
— на боковых гранях пирамиды. Так как плоскости A_{1}B_{1}C_{1}D_{1}
и ABCD
параллельны, то квадрат A_{1}B_{1}C_{1}D_{1}
вписан в квадрат K_{1}L_{1}M_{1}N_{1}
, полученный в сечении пирамиды KLMNP
плоскостью, параллельной её основанию.
Пусть точки A_{1}
, B_{1}
, C_{1}
и D_{1}
лежат на сторонах соответственно K_{1}L_{1}
, L_{1}M_{1}
, M_{1}N_{1}
и K_{1}N_{1}
квадрата K_{1}L_{1}M_{1}N_{1}
. Так как ребро куба равно x
, то пирамида K_{1}L_{1}M_{1}N_{1}P
подобна пирамиде KLMNP
с коэффициентом \frac{h-x}{h}
. Значит, сторона квадрата K_{1}L_{1}M_{1}N_{1}
равна \frac{a(h-x)}{h}
.
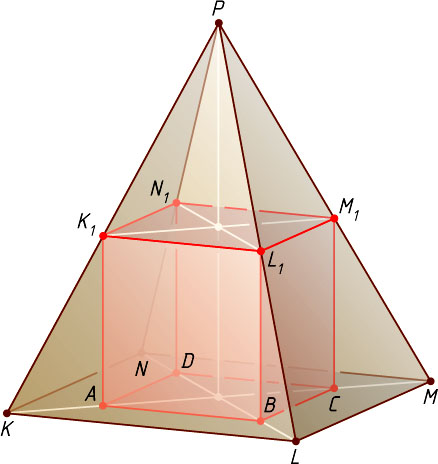
Рассмотрим случай, когда точки A_{1}
, B_{1}
, C_{1}
и D_{1}
совпадают с точками соответственно K_{1}
, L_{1}
, M_{1}
и N_{1}
(рис. 1). Тогда
a\cdot\frac{h-x}{h}=x,
откуда находим, что x=\frac{ah}{a+h}
.
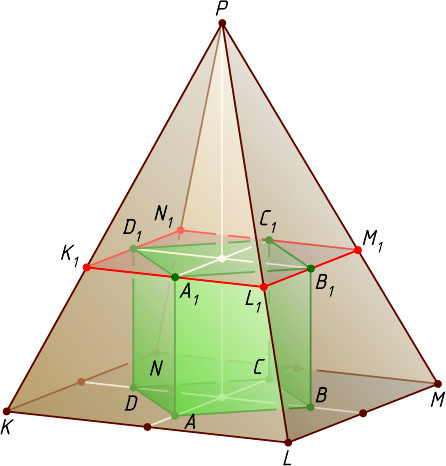
Пусть точки A_{1}
, B_{1}
, C_{1}
и D_{1}
совпадают с серединами соответствующих сторон квадрата K_{1}L_{1}M_{1}N_{1}
(рис. 2). Тогда
a\cdot\frac{h-x}{h\sqrt{2}}=x,
откуда находим, что x=\frac{ah}{a+h\sqrt{2}}
.
Докажем, что если x
— сторона произвольного куба, рассматриваемого в задаче, то
\frac{ah}{a+h\sqrt{2}}\leqslant x\leqslant\frac{ah}{a+h}.
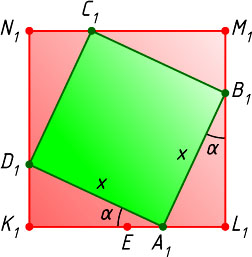
Действительно, пусть \angle A_{1}B_{1}L_{1}=\alpha
(рис. 3). Ясно, что каждому \alpha
из отрезка [0;45^{\circ}]
соответствует единственная точка A_{1}
на отрезке L_{1}E
, где E
— середина K_{1}L_{1}
. Из равных прямоугольных треугольников A_{1}L_{1}B_{1}
и D_{1}K_{1}A_{1}
находим, что
A_{1}L_{1}=A_{1}B_{1}\sin\angle A_{1}B_{1}L_{1}=x\sin\alpha,
A_{1}K_{1}=A_{1}D_{1}\cos\angle D_{1}A_{1}K_{1}=x\cos\alpha,
а так как A_{1}L_{1}+A_{1}K_{1}=K_{1}L_{1}
, то
x\sin\alpha+x\cos\alpha=a\cdot\frac{h-x}{h},
откуда находим, что
x=\frac{ah}{h(\sin\alpha+\cos\alpha)+a}=\frac{ah}{h\sqrt{2}\sin(\alpha+45^{\circ})+a}.
Если 0\leqslant\alpha\leqslant45^{\circ}
, то
\frac{\sqrt{2}}{2}\leqslant\sin(\alpha+45^{\circ})\leqslant1.
Поэтому
\frac{ah}{a+h\sqrt{2}}\leqslant\frac{ah}{h\sqrt{2}\sin(\alpha+45^{\circ})+a}\leqslant\frac{ah}{a+h}.
Следовательно, сторона куба принимает любое значение между \frac{ah}{a+h\sqrt{2}}
и \frac{ah}{a+h}
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 18(а), с. 74


