8312. Найдите ребро куба, одна грань которого лежит в плоскости основания правильной треугольной пирамиды, а четыре оставшиеся вершины — на её боковой поверхности, если стороны основания пирамиды равны a
, а высота пирамиды равна h
.
Ответ. \frac{3ah}{(2\sqrt{3}+3)h+3a}
.
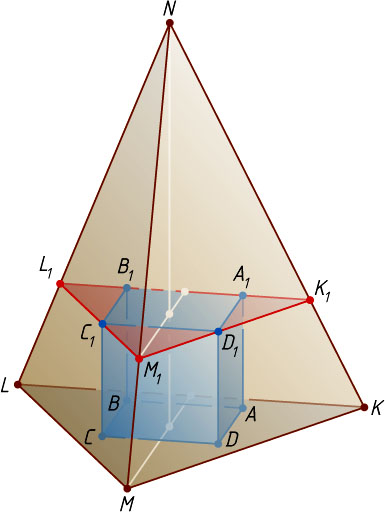
Решение. Пусть вершины A
, B
, C
и D
куба ABCDA_{1}B_{1}C_{1}D_{1}
с ребром x
лежат на основании KLM
правильной треугольной пирамиды KLMN
с вершиной N
, а вершины A_{1}
, B_{1}
, C_{1}
и D_{1}
— на боковых гранях пирамиды. Так как плоскости A_{1}B_{1}C_{1}D_{1}
и ABCD
параллельны, то квадрат A_{1}B_{1}C_{1}D_{1}
вписан в треугольник K_{1}L_{1}M_{1}
, полученный в сечении пирамиды KLMN
плоскостью, параллельной её основанию. Пусть при этом точки A_{1}
и B_{1}
лежат, например, на стороне K_{1}L_{1}
. Тогда точка C_{1}
— на стороне L_{1}M_{1}
, а точка D_{1}
— на стороне K_{1}M_{1}
.
Пусть ребро куба равно x
. Тогда пирамида K_{1}L_{1}M_{1}N
подобна пирамиде KLMN
с коэффициентом \frac{h-x}{h}
. Значит, сторона равностороннего треугольника K_{1}L_{1}M_{1}
равна \frac{a(h-x)}{h}
. Далее имеем:
B_{1}L_{1}=A_{1}K_{1}=A_{1}D_{1}\ctg\angle A_{1}K_{1}D_{1}=x\ctg60^{\circ}=\frac{x}{\sqrt{3}},
a\cdot\frac{h-x}{h}=K_{1}L_{1}=A_{1}K_{1}+A_{1}B_{1}+B_{1}L_{1}=\frac{x}{\sqrt{3}}+x+\frac{x}{\sqrt{3}}=\frac{2x}{\sqrt{3}}+x.
Из уравнения
a\cdot\frac{h-x}{h}=\frac{2x}{\sqrt{3}}+x
находим, что
x=\frac{3ah}{(2\sqrt{3}+3)h+3a}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 18(б), с. 74
