8313. Рёбра прямоугольного параллелепипеда равны a
, b
и c
. Найдите углы между его диагоналями.
Ответ. 2\arctg\frac{a}{\sqrt{b^{2}+c^{2}}}=\arccos\frac{-a^{2}+b^{2}+c^{2}}{a^{2}+b^{2}+c^{2}}
или 180^{\circ}-2\arctg\frac{a}{\sqrt{b^{2}+c^{2}}}=180^{\circ}-\arccos\frac{-a^{2}+b^{2}+c^{2}}{a^{2}+b^{2}+c^{2}}
;
2\arctg\frac{b}{\sqrt{a^{2}+c^{2}}}=\arccos\frac{a^{2}-b^{2}+c^{2}}{a^{2}+b^{2}+c^{2}}
или 180^{\circ}-2\arctg\frac{b}{\sqrt{a^{2}+c^{2}}}=180^{\circ}-\arccos\frac{a^{2}-b^{2}+c^{2}}{a^{2}+b^{2}+c^{2}}
;
2\arctg\frac{c}{\sqrt{a^{2}+b^{2}}}=\arccos\frac{a^{2}+b^{2}-c^{2}}{a^{2}+b^{2}+c^{2}}
или 180^{\circ}-2\arctg\frac{c}{\sqrt{a^{2}+b^{2}}}=180^{\circ}-\arccos\frac{a^{2}+b^{2}-c^{2}}{a^{2}+b^{2}+c^{2}}
.
Решение. Первый способ. Пусть ABCDA_{1}B_{1}C_{1}D_{1}
— прямоугольный параллелепипед, в котором AA_{1}\parallel BB_{1}\parallel CC_{1}\parallel DD_{1}
, AB=a
, AD=b
, AA_{1}=c
, а диагонали пересекаются в точке O
. Найдём угол между диагоналями A_{1}C
и B_{1}D
.
Рассмотрим сечение параллелепипеда плоскостью A_{1}DCB_{1}
. Получим прямоугольник A_{1}DCB_{1}
, диагонали A_{1}C
и B_{1}D
которого пересекаются в точке O
. Так как A_{1}OB_{1}
— внешний угол равнобедренного треугольника B_{1}OC
, то \angle A_{1}OB_{1}=2\angle B_{1}CO
. Из прямоугольного треугольника A_{1}CB_{1}
находим, что
\tg\angle B_{1}CO=\frac{A_{1}B_{1}}{B_{1}C}=\frac{a}{\sqrt{b^{2}+c^{2}}}.
Значит,
\angle B_{1}CO=\arctg\frac{a}{\sqrt{b^{2}+c^{2}}},~\angle A_{1}OB_{1}=2\arctg\frac{a}{\sqrt{b^{2}+c^{2}}}.
Если a^{2}\leqslant b^{2}+c^{2}
, то
\frac{a}{\sqrt{b^{2}+c^{2}}}\leqslant1,~\angle B_{1}CO\leqslant45^{\circ},~\angle A_{1}OB_{1}\leqslant90^{\circ}.
В этом случае угол между диагоналями A_{1}C
и B_{1}D
параллелепипеда равен углу \angle A_{1}OB_{1}
. Если же a^{2}\gt b^{2}+c^{2}
, то угол между диагоналями A_{1}C
и B_{1}D
равен углу, смежному с углом A_{1}OB_{1}
, т.е
\angle B_{1}OC=180^{\circ}-2\arctg\frac{a}{\sqrt{b^{2}+c^{2}}}.
Аналогично находятся остальные углы.
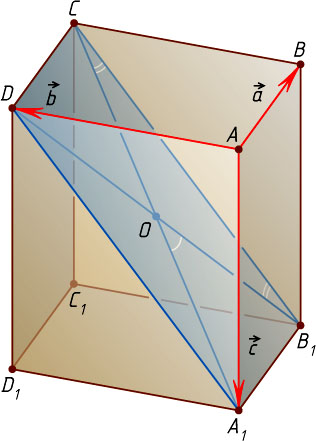
Второй способ. Пусть ABCDA_{1}B_{1}C_{1}D_{1}
— прямоугольный параллелепипед, в котором AA_{1}\parallel BB_{1}\parallel CC_{1}\parallel DD_{1}
, AB=a
, AD=b
, AA_{1}=c
Обозначим \overrightarrow{AB}=\overrightarrow{a}
, \overrightarrow{AD}=\overrightarrow{b}
, \overrightarrow{AA_{1}}=\overrightarrow{c}
. Тогда
\overrightarrow{A_{1}C}=\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c},~\overrightarrow{B_{1}D}=-\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}.
Если \alpha
— угол между диагоналями A_{1}C
и B_{1}D
, то
\cos\alpha=\frac{|\overrightarrow{A_{1}C}\cdot\overrightarrow{B_{1}D}|}{A_{1}C\cdot B_{1}D}=\frac{|(\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c})\cdot(-\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c})|}{\sqrt{a^{2}+b^{2}+c^{2}}\cdot\sqrt{a^{2}+b^{2}+c^{2}}}=\frac{|-a^{2}+b^{2}+c^{2}|}{a^{2}+b^{2}+c^{2}}.
Следовательно, если a^{2}\leqslant b^{2}+c^{2}
, то
\alpha=\arccos\frac{-a^{2}+b^{2}+c^{2}}{a^{2}+b^{2}+c^{2}}.
Если же a^{2}\gt b^{2}+c^{2}
, то
\alpha=180^{\circ}-\arccos\frac{-a^{2}+b^{2}+c^{2}}{a^{2}+b^{2}+c^{2}}.
Остальное аналогично.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 19(а), с. 74
