8314. Рёбра прямоугольного параллелепипеда равны a
, b
и c
. Найдите угол между диагональю параллелепипеда и скрещивающейся с ней диагональю грани со сторонами a
и b
.
Ответ. \arccos\frac{|a^{2}-b^{2}|}{\sqrt{(a^{2}+b^{2})(a^{2}+b^{2}+c^{2})}}
.
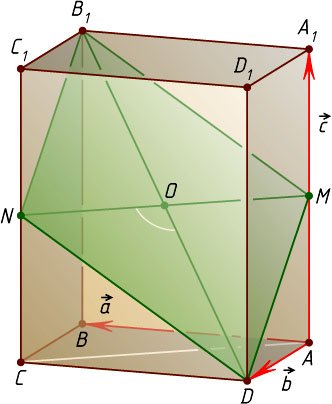
Решение. Первый способ. Пусть ABCDA_{1}B_{1}C_{1}D_{1}
— прямоугольный параллелепипед, в котором AA_{1}\parallel BB_{1}\parallel CC_{1}\parallel DD_{1}
, AB=a
, AD=b
, AA_{1}=c
. Найдём угол между диагональю B_{1}D
параллелепипеда и диагональю AC
грани ABCD
.
Пусть M
и N
— середины рёбер AA_{1}
и CC_{1}
. Прямые MN
и B_{1}D
пересекаются в центре O
параллелепипеда. Проведём сечение параллелепипеда плоскостью, проходящей через пересекающиеся прямые B_{1}D
и NM
. Получим параллелограмм B_{1}MDN
. Так как MN\parallel AC
, то угол между скрещивающимися прямыми B_{1}D
и AC
равен углу между диагоналями B_{1}D
и NM
параллелограмма B_{1}MDN
. По теореме косинусов из треугольника NOD
находим, что
\cos\angle NOD=\frac{ON^{2}+OD^{2}-ND^{2}}{2ON\cdot OD}=\frac{\left(\frac{AC}{2}\right)^{2}+\left(\frac{B_{1}D}{2}\right)^{2}-ND^{2}}{2\cdot\frac{AC}{2}\cdot\frac{B_{1}D}{2}}=
=\frac{\frac{a^{2}+b^{2}}{4}+\frac{a^{2}+b^{2}+c^{2}}{4}-a^{2}-\frac{c^{2}}{4}}{\sqrt{a^{2}+b^{2}}\cdot\frac{1}{2}\sqrt{a^{2}+b^{2}+c^{2}}}=\frac{b^{2}-a^{2}}{\sqrt{(a^{2}+b^{2})(a^{2}+b^{2}+c^{2})}}.
Пусть \beta
угол между прямыми B_{1}D
и AC
. Если a\leqslant b
, то
\beta=\arccos\frac{b^{2}-a^{2}}{\sqrt{(a^{2}+b^{2})(a^{2}+b^{2}+c^{2})}}.
Если же a\gt b
, то
\beta=\arccos\frac{a^{2}-b^{2}}{\sqrt{(a^{2}+b^{2})(a^{2}+b^{2}+c^{2})}}.
Второй способ. Пусть ABCDA_{1}B_{1}C_{1}D_{1}
— прямоугольный параллелепипед, в котором AA_{1}\parallel BB_{1}\parallel CC_{1}\parallel DD_{1}
, AB=a
, AD=b
, AA_{1}=c
. Обозначим \overrightarrow{AB}=\overrightarrow{a}
, \overrightarrow{AD}=\overrightarrow{b}
, \overrightarrow{AA_{1}}=\overrightarrow{c}
. Тогда
\overrightarrow{AC}=\overrightarrow{a}+\overrightarrow{b},~\overrightarrow{B_{1}D}=-\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}.
Если \beta
— угол между прямыми AC
и B_{1}D
, то
\cos\beta=\frac{|\overrightarrow{AC}\cdot\overrightarrow{B_{1}D}|}{AC\cdot B_{1}D}=\frac{|(\overrightarrow{a}+\overrightarrow{b})\cdot(-\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c})|}{\sqrt{a^{2}+b^{2}}\cdot\sqrt{a^{2}+b^{2}+c^{2}}}=\frac{|a^{2}-b^{2}|}{\sqrt{(a^{2}+b^{2})(a^{2}+b^{2}+c^{2})}}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 19(б), с. 74
