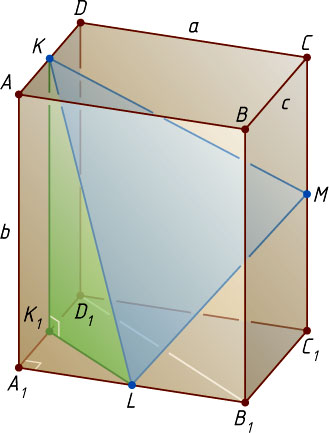
8316. Пусть K
, L
и M
— середины рёбер соответственно AD
, A_{1}B_{1}
и CC_{1}
прямоугольного параллелепипеда ABCDA_{1}B_{1}C_{1}D_{1}
, в котором AB=a
, AA_{1}=b
, AD=c
. Найдите отношение суммы квадратов сторон треугольника KLM
к квадрату диагонали параллелепипеда.
Ответ. \frac{3}{2}
.
Решение. Пусть K_{1}
— ортогональная проекция точки K
на плоскость грани A_{1}B_{1}C_{1}D_{1}
. Тогда K_{1}
— середина ребра A_{1}D_{1}
, KK_{1}=AA_{1}=b
, а K_{1}L
— средняя линия треугольника B_{1}A_{1}D_{1}
. Из прямоугольных треугольников B_{1}A_{1}D_{1}
и KK_{1}L
находим, что
B_{1}D_{1}^{2}=A_{1}B_{1}^{2}+A_{1}D_{1}^{2}=a^{2}+c^{2},~KL^{2}=\frac{1}{4}B_{1}D_{1}^{2}=\frac{1}{4}(a^{2}+c^{2}),
KL^{2}=KK_{1}^{2}+K_{1}L^{2}=b^{2}+\frac{a^{2}+c^{2}}{4}=\frac{4b^{2}+a^{2}+c^{2}}{4}.
Аналогично,
KM^{2}=\frac{4a^{2}+b^{2}+c^{2}}{4},~LM^{2}=\frac{4c^{2}+a^{2}+b^{2}}{4},
а так как DB_{1}^{2}=a^{2}+b^{2}+c^{2}
, то
\frac{KL^{2}+KM^{2}+LM^{2}}{DB_{1}^{2}}=\frac{\frac{4b^{2}+a^{2}+c^{2}}{4}+\frac{4a^{2}+b^{2}+c^{2}}{4}+\frac{4c^{2}+a^{2}+b^{2}}{4}}{a^{2}+b^{2}+c^{2}}=
=\frac{6a^{2}+6b^{2}+6c^{2}}{4(a^{2}+b^{2}+c^{2})}=\frac{3}{2}.