8324. Постройте изображение параллелепипеда ABCDA_{1}B_{1}C_{1}D_{1}
, если даны изображения точек A
, C
, B_{1}
и D_{1}
.
Решение. Будем считать, что точки A
, B
, C
, D
, A_{1}
, B_{1}
, C_{1}
, D_{1}
и есть изображения вершин параллелепипеда. Пусть точки A
, C
, B_{1}
и D_{1}
даны. Строим середины M
и M_{1}
отрезков соответственно AC
и B_{1}D_{1}
. Через точку M
проводим прямую a
, параллельную B_{1}D_{1}
, а через точку M_{1}
— прямую b
, параллельную AC
. На прямой a
откладываем от точки M
по разные стороны от неё отрезки MB
и MD
, равные половине B_{1}D_{1}
, на прямой b
от точки M_{1}
по разные стороны от неё откладываем отрезки M_{1}A_{1}
и M_{1}C_{1}
, равные половине AC
. При этом точки B
и B_{1}
, лежащие в плоскости DBB_{1}D_{1}
, должны располагаться по одну сторону от прямой MM_{1}
.
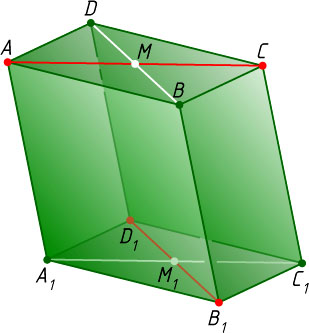
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 25(в), с. 75
