8325. Постройте изображение параллелепипеда ABCDA_{1}B_{1}C_{1}D_{1}
, если даны изображения середин отрезков AB_{1}
, BC_{1}
, CD
и A_{1}D_{1}
.
Решение. Будем считать, что точки A
, B
, C
, D
, A_{1}
, B_{1}
, C_{1}
, D_{1}
и есть изображения вершин параллелепипеда. Предположим, что изображение ABCDA_{1}B_{1}C_{1}D_{1}
параллелепипеда построено, а точки K
, L
, M
и N
— середины отрезков AB_{1}
, BC_{1}
, CD
и A_{1}D_{1}
соответственно. Тогда KL
— средняя линия треугольника BA_{1}C_{1}
. Поэтому KL\parallel A_{1}C_{1}
и KL=\frac{1}{2}A_{1}C_{1}
.
Если F
— середина C_{1}D_{1}
, то FN
— средняя линия треугольника A_{1}D_{1}C_{1}
. Поэтому FN\parallel A_{1}C_{1}
и FN=\frac{1}{2}A_{1}C_{1}
. Значит, NF\parallel KL
и NF=KL
. Следовательно, четырёхугольник KNFL
— параллелограмм. Аналогично докажем, что если E
— середина AD
, то четырёхугольник KLME
— параллелограмм. Изображения AA_{1}
, BB_{1}
, CC_{1}
и DD_{1}
боковых рёбер параллелепипеда, а также отрезки, соединяющие середины AB
и A_{1}B_{1}
, равны и параллельны отрезкам MF
и NE
. Отсюда вытекает следующее построение.
Достроив треугольники KLN
и KLM
до параллелограммов KLFN
и KLME
, получим середины F
и E
рёбер C_{1}D_{1}
и AD
соответственно. Через точку K
проведём прямую, параллельную NE
, и отложим на ней по разные стороны от точки K
отрезки KP
и KQ
, равные половине NE
. Получим середины P
и Q
отрезков AB
и A_{1}B_{1}
. Аналогично построим середины G
и H
отрезков BC
и B_{1}C_{1}
соответственно. Таким образом, осталось построить параллелограмм ABCD
по серединам M
, E
, P
и G
его сторон. Для этого через точки M
и P
проведём прямые, параллельные EG
, а через точки E
и G
— прямые, параллельные MP
. Аналогично строится параллелограмм A_{1}B_{1}C_{1}D_{1}
.
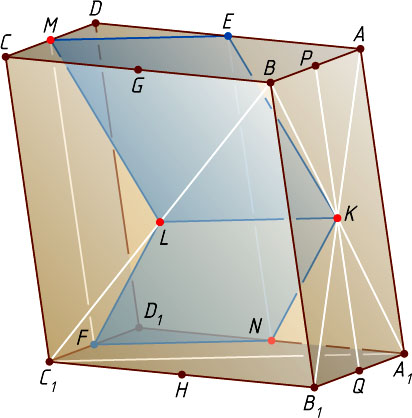
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 25(г), с. 75
