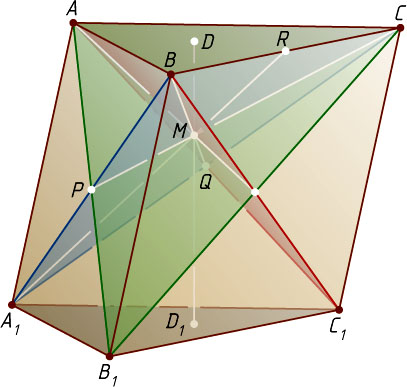
8327. Дано изображение призмы ABCA_{1}B_{1}C_{1}
. Постройте изображение точки M
пересечения плоскостей A_{1}BC
, AB_{1}C
и ABC_{1}
. Пусть высота призмы равна h
. Найдите расстояние от точки M
до оснований призмы.
Ответ. \frac{1}{3}h
; \frac{2}{3}h
.
Решение. Будем считать, что точки A
, B
, C
, A_{1}
, B_{1}
, C_{1}
, M
и есть изображения вершин призмы. Пусть P
и Q
— центры граней AA_{1}B_{1}B
и AA_{1}C_{1}C
. Точки C
и P
— общие точки плоскостей A_{1}BC
и AB_{1}C
, поэтому плоскости A_{1}BC
и AB_{1}C
пересекаются по прямой CP
. Точки B
и Q
— общие точки плоскостей A_{1}BC
и ABC_{1}
, поэтому плоскости A_{1}BC
и ABC_{1}
пересекаются по прямой BQ
. Прямые CP
и BQ
лежат в плоскости A_{1}BC
. Точка M
их пересечения есть точка пересечения плоскостей A_{1}BC
, AB_{1}C
и ABC_{1}
. Так как P
— середина A_{1}B
, а Q
— середина A_{1}C
, то CP
и BQ
— медианы треугольника A_{1}BC
. Значит, M
— точка пересечения медиан треугольника A_{1}BC
.
Пусть D
и D_{1}
— ортогональные проекции точки M
на параллельные плоскости соответственно ABC
и A_{1}B_{1}C_{1}
. Тогда DD_{1}
— высота призмы. Медиана A_{1}R
треугольника A_{1}BC
делится точкой M
в отношении 2:1
. Отрезки A_{1}R
и D_{1}D
с концами в параллельных плоскостях A_{1}B_{1}C_{1}
и ABC
пересекаются в точке M
. Значит, D_{1}M:DM=2:1
. Следовательно,
DM=\frac{1}{3}DD_{1}=\frac{1}{3}h,~D_{1}M=\frac{2}{3}DD_{1}=\frac{2}{3}h.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 26, с. 75
