8328. Измерения прямоугольного параллелепипеда равны a
, b
и c
(a\lt b\lt c
). Некоторое его сечение является квадратом. Найдите сторону этого квадрата.
Ответ. a
или b
или c
, если c\leqslant\sqrt{a^{2}+b^{2}}
;
a
или b
, если c\gt\sqrt{a^{2}+b^{2}}
.
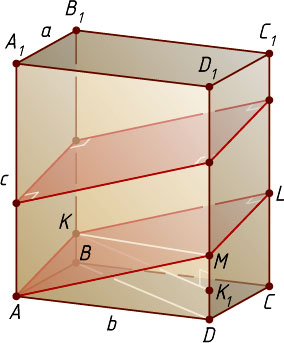
Решение. Рассмотрим прямоугольный параллелепипед ABCDA_{1}B_{1}C_{1}D_{1}
, в котором AB=a
, AD=b
, AA_{1}=c
, причём a\lt b\lt c
. Через вершину A
проведём плоскость, параллельную плоскости сечения, являющегося квадратом. Пусть проведённая плоскость пересекает прямые BB_{1}
, CC_{1}
и DD_{1}
соответственно в точках K
, L
и M
. Тогда AKLM
— квадрат, равный квадрату сечения.
Обозначим через x
сторону квадрата. Тогда KM=x\sqrt{2}
. Из прямоугольных треугольников ABK
и ADM
находим, что
BK=\sqrt{AK^{2}-AB^{2}}=\sqrt{x^{2}-a^{2}},
DM=\sqrt{AM^{2}-AD^{2}}=\sqrt{x^{2}-b^{2}}.
Пусть K_{1}
— ортогональная проекция точки K
на прямую DD_{1}
. Тогда
MK^{2}=|DM-BK|^{2}+BD^{2},
или
2x^{2}=|\sqrt{x^{2}-a^{2}}-\sqrt{x^{2}-b^{2}}|^{2}+a^{2}+b^{2},
откуда следует, что x=a
или x=b
.
Проведя плоскость, параллельную данному сечению, через вершину B
, аналогично получим, что x=a
или x=c
.
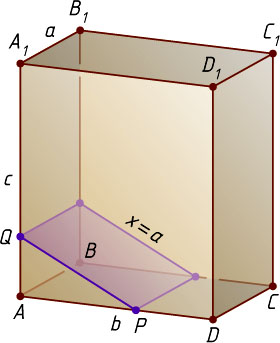
Пусть x=a
. Возьмём на рёбрах AD
и AA_{1}
соответственно точки P
и Q
, для которых PQ=a
(это можно сделать, так как a\lt b
). Тогда сечение параллелепипеда плоскостью, проходящей через точки P
и Q
параллельно ребру AB
, есть квадрат со стороной a
.
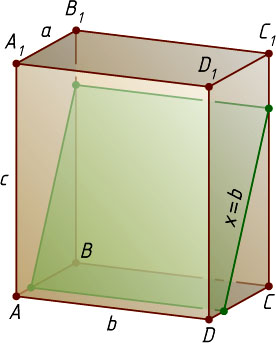
Аналогично строится секущая плоскость для x=b
.
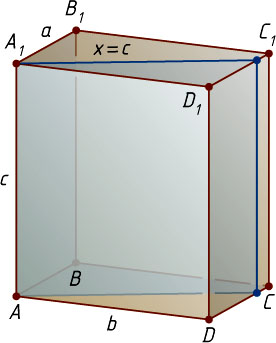
Пусть x=c
и при этом c\leqslant\sqrt{a^{2}+b^{2}}
. Тогда секущая плоскость строится также аналогично. Если же c\gt\sqrt{a^{2}+b^{2}}
, то в сечении параллелепипеда плоскостью не может получиться квадрат со стороной c
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 28, с. 75



