8329. Пусть проекция вершины A
параллелепипеда ABCDA_{1}B_{1}C_{1}D_{1}
на некоторую плоскость лежит внутри проекции на эту плоскость треугольника A_{1}BD
. Докажите, что площадь проекции параллелепипеда в два раза больше площади проекции треугольника A_{1}BD
.
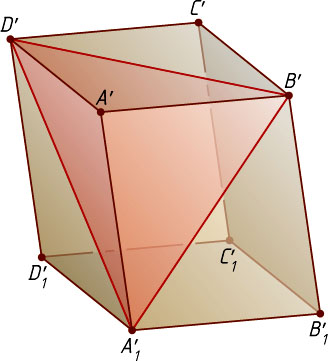
Решение. Пусть A'
, B'
, C'
, D'
, A_{1}'
, B_{1}'
, C_{1}'
и D_{1}'
— параллельные проекции вершин соответственно A
, B
, C
, D
, A_{1}
, B_{1}
, C_{1}
и D_{1}
параллелепипеда ABCDA_{1}B_{1}C_{1}D_{1}
, причём точка A'
лежит внутри треугольника A_{1}'B'D'
. Так как при параллельном проектировании сохраняется параллельность прямых, то четырёхугольники A'B'B_{1}'A_{1}'
, A'B'C'D'
и A'D'D_{1}'A_{1}'
— параллелограммы. Они делятся своими диагоналями B'A_{1}'
, B'D'
и D'A_{1}'
на равные треугольники. Так как точка A'
лежит внутри треугольника A_{1}'B'D'
, то каждые два из этих параллелограммов имеют ровно одну общую сторону, а их объединение (шестиугольник A_{1}'B_{1}'B'C'D'D_{1}'
) есть проекция данного параллелепипеда на плоскость \alpha
. Следовательно,
S'=S_{A_{1}'B_{1}'B'C'D'D_{1}'}=2S_{\triangle A_{1}'B'D'}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 29, с. 75
