8330. Найдите наибольшее значение площади ортогональной проекции прямоугольного параллелепипеда с измерениями a
, b
и c
на некоторую плоскость.
Ответ. \sqrt{a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2}}
.
Решение. Докажем сначала следующее утверждение. Если проекция вершины A
параллелепипеда ABCDA_{1}B_{1}C_{1}D_{1}
на некоторую плоскость лежит внутри проекции на эту плоскость треугольника A_{1}BD
, то площадь проекции параллелепипеда в два раза больше площади проекции треугольника A_{1}BD
.
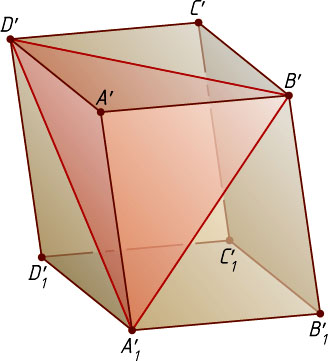
Пусть A'
, B'
, C'
, D'
, A_{1}'
, B_{1}'
, C_{1}'
и D_{1}'
— параллельные проекции вершин соответственно A
, B
, C
, D
, A_{1}
, B_{1}
, C_{1}
и D_{1}
параллелепипеда ABCDA_{1}B_{1}C_{1}D_{1}
, (рис. 1) причём точка A'
лежит внутри треугольника A_{1}'B'D'
. Так как при параллельном проектировании сохраняется параллельность прямых, то четырёхугольники A'B'B_{1}'A_{1}'
, A'B'C'D'
и A'D'D_{1}'A_{1}'
— параллелограммы. Они делятся своими диагоналями B'A_{1}'
, B'D'
и D'A_{1}'
на равные треугольники. Так как точка A'
лежит внутри треугольника A_{1}'B'D'
, то каждые два из этих параллелограммов имеют ровно одну общую сторону, а их объединение (шестиугольник A_{1}'B_{1}'B'C'D'D_{1}'
) есть проекция данного параллелепипеда на плоскость \alpha
. Следовательно,
S'=S_{A_{1}'B_{1}'B'C'D'D_{1}'}=2S_{\triangle A_{1}'B'D'}.
Пусть теперь A'B'C'D'A_{1}'B_{1}'C_{1}'D_{1}'
— ортогональная проекция прямоугольного параллелепипеда ABCDA_{1}B_{1}C_{1}D_{1}
(AB=a
, AD=b
, AA_{1}=c
) на некоторую плоскость. Обозначим через \varphi
угол между этой плоскостью и плоскостью треугольника A_{1}BD
. По ранее доказанному
S'=S_{A'B'C'D'A_{1}'B_{1}'C_{1}'D_{1}'}=2S_{\triangle A_{1}'B'D'}=2S_{\triangle A_{1}BD}\cos\varphi\leqslant2S_{\triangle A_{1}BD},
причём равенство достигается, если \varphi=0^{\circ}
, т. е. когда плоскость проекций параллельна плоскости треугольника A_{1}BD
.
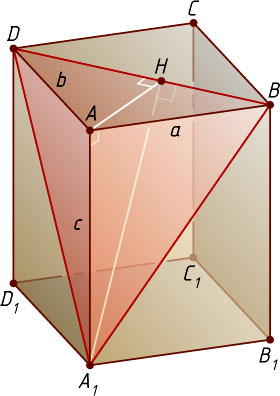
Для нахождения площади треугольника A_{1}BD
опустим перпендикуляр A_{1}H
из вершины A_{1}
на прямую BD
(рис. 2). По теореме о трёх перпендикулярах AH
— высота прямоугольного треугольника ABD
. Поэтому
AH=\frac{AB\cdot AD}{BD}=\frac{ab}{\sqrt{a^{2}+b^{2}}},
A_{1}H=\sqrt{A_{1}A^{2}+AH^{2}}=\sqrt{c^{2}+\frac{a^{2}b^{2}}{a^{2}+b^{2}}}=\frac{\sqrt{a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2}}}{\sqrt{a^{2}+b^{2}}},
S_{\triangle A_{1}BD}=\frac{1}{2}BD\cdot A_{1}H=\frac{1}{2}\sqrt{a^{2}+b^{2}}\cdot\frac{\sqrt{a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2}}}{\sqrt{a^{2}+b^{2}}}=
=\frac{1}{2}\sqrt{a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2}}.
Следовательно,
S_{\max}=2S_{\triangle A_{1}BD}=\sqrt{a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2}}.
Ясно, что если ортогональная проекция точки A
лежит вне ортогональной проекции треугольника A_{1}BD
на некоторую плоскость, то площадь ортогональной проекции параллелепипеда на эту плоскость будет меньше найденной.
Источник: Прасолов В. В., Шарыгин И. Ф. Задачи по стереометрии. — М.: Наука, 1989. — № 11.11, с. 208
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 30, с. 76
Источник: Шарыгин И. Ф. Геометрия. Стереометрия: Задачник для 10—11 кл. — М.: Дрофа, 1998. — № 259, с. 36

