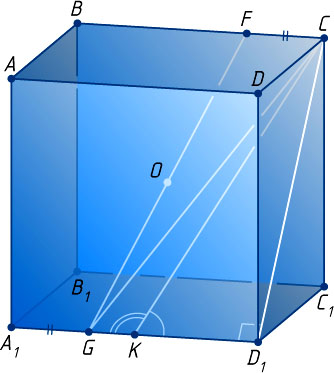
8331. Через центр единичного куба проведена плоскость, не проходящая через ребро куба и делящая куб на два многогранника. Докажите, что в каждом из получившихся многогранников найдётся диагональ, длина которой не меньше \frac{3}{2}
.
Решение. Пусть K
— середина ребра A_{1}D_{1}
единичного куба ABCDA_{1}B_{1}C_{1}D_{1}
. Тогда
CK=\sqrt{KD_{1}^{2}+D_{1}C_{1}^{2}+C_{1}C^{2}}=\sqrt{\frac{1}{4}+1+1}=\frac{3}{2}.
Куб симметричен относительно его центра O
. Пусть секущая плоскость проходит через точку F
ребра BC
, не совпадающую с серединой этого ребра. Тогда она пересекает ребро в точке G
, симметричной точке F
относительно центра O
.
Предположим, что середина K
ребра A_{1}D_{1}
и точка C
лежат в одном полупространстве, на которые секущая плоскость делит всё пространство. Докажем, что диагональ CG
одного из получившихся многогранников меньше CK
. Действительно, в прямоугольном треугольнике CD_{1}K
угол CKD_{1}
— острый, поэтому смежный с ним угол CKG
— тупой. Значит, CG
— наибольшая сторона треугольника CKG
. Следовательно, CG\gt CK=\frac{3}{2}
.
Если же точки K
и C
лежат по разные стороны от секущей плоскости, то в одном полупространстве лежат точки K
и B
. Для диагонали BG
одного из получившихся многогранников верно неравенство BG\gt BK=CK\gt\frac{3}{2}
.
Если секущая плоскость проходит через середину ребра BC
, то отрезок KC=\frac{3}{2}
— диагональ одного из получившихся многогранников.
Аналогично для случаев, когда вместо точки F
ребра BC
взята точка любого другого ребра куба.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. —
