8335. Найдите площадь сечения шара радиуса 3 плоскостью, удалённой от его центра на расстояние, равное 2.
Ответ. 5\pi
.
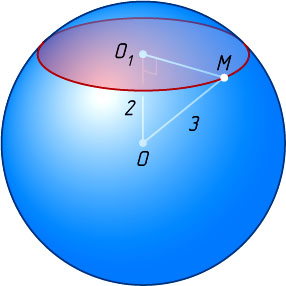
Решение. Пусть O
— центр данного шара, O_{1}
— основание перпендикуляра, опущенного из точки O
на плоскость сечения. Тогда O_{1}
— центр круга, являющегося сечением шара. Пусть M
— произвольная точка окружности этого круга, r
— радиус круга, S
— площадь. Тогда O_{1}M
— радиус сечения. По теореме Пифагора из прямоугольного треугольника OO_{1}M
находим, что
O_{1}M^{2}=OM^{2}-OO_{1}^{2}=9-4=5.
Следовательно,
S=\pi r^{2}=\pi\cdot O_{1}M^{2}=5\pi.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 4, с. 81
