8336. Осевым сечением конуса является равнобедренный прямоугольный треугольник с гипотенузой, равной 2. Через вершину конуса проведено сечение, образующее угол \alpha
с плоскостью основания. Найдите площадь сечения.
Ответ. \frac{\sqrt{-\cos2\alpha}}{\sin^{2}\alpha}
.
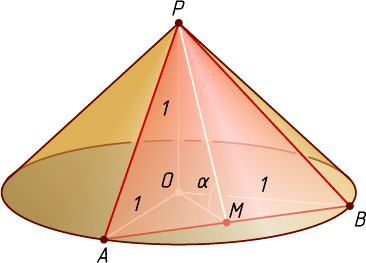
Решение. Пусть P
— вершина конуса, O
— центр основания, AB
— хорда основания, лежащая в секущей плоскости, M
— середина AB
. Тогда AOB
и APB
— равнобедренные треугольники с общим основанием AB
. Поэтому OM\perp AB
и PM\perp AB
. Значит, OMP
— линейный угол двугранного угла между плоскостями основания и сечения. По условию задачи \angle OMP=\alpha
. Так как угол при вершине осевого сечения конуса равен 90^{\circ}
, то OA=OB=OP=1
. Далее имеем:
OM=OP\ctg\alpha,
AM=\sqrt{OA^{2}-OM^{2}}=\sqrt{1-\ctg^{2}\alpha}=\frac{\sqrt{-\cos2\alpha}}{\sin\alpha},
PM=\frac{OP}{\sin\alpha}=\frac{1}{\sin\alpha}.
Следовательно,
S_{\triangle APB}=\frac{1}{2}AB\cdot PM=\frac{\sqrt{-\cos2\alpha}}{\sin\alpha}\cdot\frac{1}{\sin\alpha}=\frac{\sqrt{-\cos2\alpha}}{\sin^{2}\alpha}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 5, с. 85
