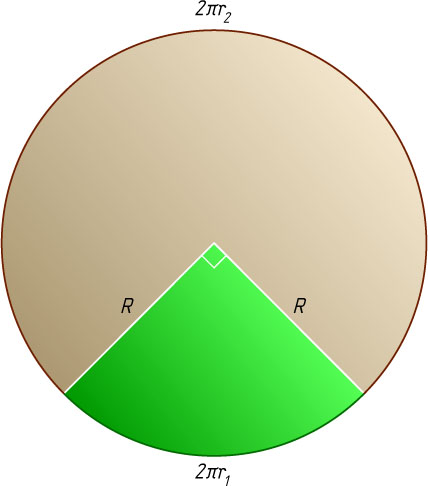
8337. Из круга вырезан сектор, представляющий собой четверть круга. Из этого сектора и из оставшейся части круга изготовлены боковые поверхности двух конусов. Найдите отношение высот этих конусов.
Ответ. \frac{\sqrt{15}}{\sqrt{7}}
.
Решение. Пусть R
— радиус данного круга, r_{1}
и r_{2}
— радиусы оснований полученных конусов (r_{1}\lt r_{2}
), h_{1}
и h_{2}
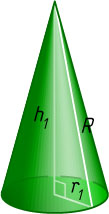
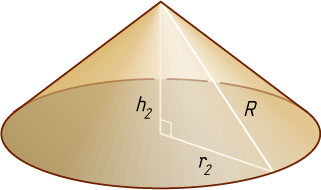
— высоты конусов. Тогда образующая каждого из полученных конусов равна R
. Длины окружностей оснований конусов равны соответственно четверти и трём четвертям длины окружности радиуса R
. Из уравнений
2\pi r_{1}=\frac{1}{4}\cdot2\pi R,~2\pi r_{2}=\frac{3}{4}\cdot2\pi R
находим, что
r_{1}=\frac{1}{4}R,~r_{2}=\frac{3}{4}R.
Рассмотрим осевые сечения конусов. По теореме Пифагора находим, что
h_{1}=\sqrt{R^{2}-r_{1}^{2}}=\sqrt{R^{2}-\frac{R^{2}}{16}}=\frac{R\sqrt{15}}{4},
h_{2}=\sqrt{R^{2}-r_{2}^{2}}=\sqrt{R^{2}-\frac{9R^{2}}{16}}=\frac{R\sqrt{7}}{4}.
Следовательно, \frac{h_{1}}{h_{2}}=\frac{\sqrt{15}}{\sqrt{7}}
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 6, с. 82


