8338. Сфера радиуса 2 пересечена плоскостью, удалённой от центра на расстояние 1. Найдите длину кратчайшего пути по поверхности сферы между двумя наиболее удалёнными точками сечения.
Ответ. \frac{4\pi}{3}
.
Указание. Кратчайшим путём по сфере, соединяющим две её точки A
и B
, является меньшая из двух дуг AB
окружности большого круга, проходящей через точки A
и B
.
Решение. Кратчайшим путём по сфере, соединяющим две её точки A
и B
, является меньшая из двух дуг AB
окружности большого круга, проходящей через точки A
и B
.
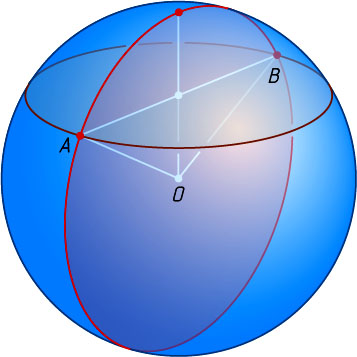
Данное сечение сферы плоскостью есть окружность. Наиболее удалённые точки этой окружности — это любые две диаметрально противоположные точки A
и B
. Через точки A
, B
и центр O
сферы проведём плоскость. В сечении сферы этой плоскостью получим окружность радиуса 2. Хорда AB
этой окружности удалена от её центра O
на расстояние 1. Значит, меньшая из дуг AB
этой окружности видна из точки O
под углом в 120^{\circ}
. Поэтому длина этой дуги равна третьей части длины окружности радиуса 2, т. е. \frac{4\pi}{3}
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 7, с. 82
