8339. Найдите площадь осевого сечения тела, полученного при вращении правильного треугольника со стороной a
вокруг прямой, проходящей через его центр параллельно одной из сторон.
Ответ. \frac{a^{2}\sqrt{3}}{3}
.
Решение. Пусть ABC
— данный равносторонний треугольник со стороной a
, O
— его центр, а ось вращения проходит через точку O
параллельно BC
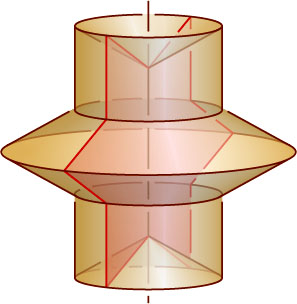
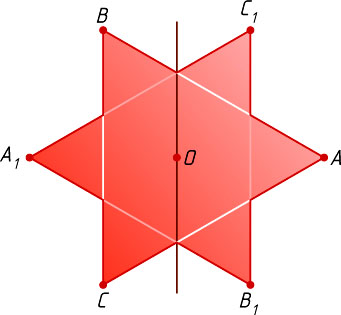
. Тогда осевое сечение полученного тела вращения есть объединение треугольника ABC
и равного ему треугольника A_{1}B_{1}C_{1}
с тем же центром O
и стороной B_{1}C_{1}
, параллельной BC
. Площадь S
этого сечения равна сумме площадей треугольника ABC
и трёх равносторонних треугольников со сторонами \frac{a}{3}
. Следовательно,
S=\frac{a^{2}\sqrt{3}}{4}+3\cdot\frac{1}{9}\cdot\frac{a^{2}\sqrt{3}}{4}=\frac{a^{2}\sqrt{3}}{4}+\frac{1}{3}\cdot\frac{a^{2}\sqrt{3}}{4}=\frac{a^{2}\sqrt{3}}{3}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 8, с. 82

