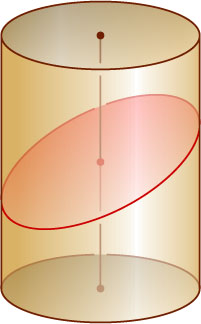
8340. Радиус основания цилиндра равен r
. Плоскость пересекает боковую поверхность цилиндра, не пересекает его оснований и образует угол \alpha
с плоскостью основания. Найдите площадь сечения цилиндра этой плоскостью.
Ответ. \frac{\pi r^{2}}{\cos\alpha}
.
Указание. Площадь ортогональной проекции плоской фигуры на плоскость равна площади проектируемой фигуры, умноженной на косинус угла между плоскостью проектируемой фигуры и плоскостью проекций.
Решение. Основание цилиндра есть ортогональная проекция данного сечения на плоскость основания. Следовательно, площадь сечения равна площади основания, делённой на косинус угла между плоскостями сечения и основания, т. е. \frac{\pi r^{2}}{\cos\alpha}
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 9, с. 82
