8342. Правильная четырёхугольная пирамида вращается вокруг прямой, проходящей через её вершину параллельно плоскости основания. Найдите площадь осевого сечения получившегося тела вращения, если сторона основания пирамиды равна a
, а высота равна h
.
Ответ. a(\sqrt{4h^{2}+a^{2}}-h)
.
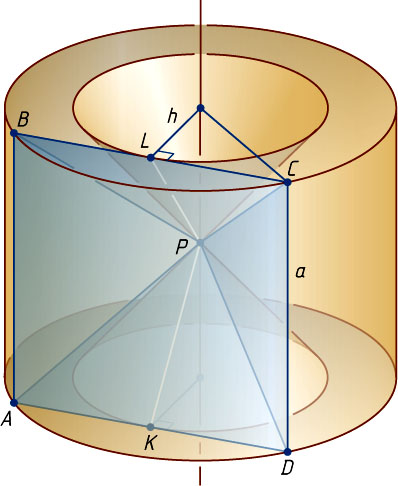
Решение. Пусть PABCD
— правильная четырёхугольная пирамида с вершиной P
, а прямая l
проходит через точку P
параллельно AB
(рис. 1). Тогда при вращении вокруг прямой l
основание H
высоты PH
пирамиды опишет окружность с центром P
радиуса h
; отрезок, соединяющий середины AD
и BC
, — боковую поверхность цилиндра с высотой a
и радиусом основания h
; отрезки AB
и CD
— боковую поверхность цилиндра с высотой a
и радиусом основания \sqrt{h^{2}+\frac{a^{2}}{4}}
; апофемы PK
и PL
— боковые поверхности двух конусов с высотой \frac{a}{2}
, лежащей на оси вращения, общей вершиной P
и радиусом основания h
.
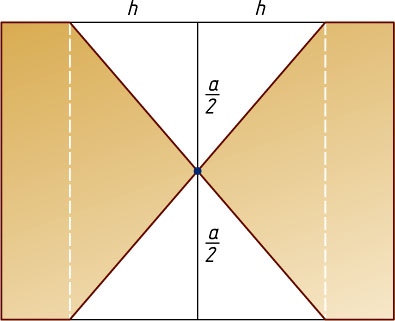
Осевое сечение полученного тела вращения есть прямоугольник со сторонами a
и 2\sqrt{h^{2}+\frac{a^{2}}{4}}
без двух равнобедренных треугольников с основаниями 2h
и высотой \frac{a}{2}
(рис. 2). Следовательно, площадь сечения равна
a\cdot2\sqrt{h^{2}+\frac{a^{2}}{4}}-2\cdot\frac{1}{2}\cdot2h\cdot\frac{a}{2}=2a\sqrt{h^{2}+\frac{a^{2}}{4}}-ah=a(\sqrt{4h^{2}+a^{2}}-h).
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 11, с. 82

