8343. На плоскости изображена окружность и две точки A
и B_{1}
, причём точка A
лежит внутри окружности. Известно, что окружность является окружностью основания некоторого конуса, точка A
лежит на основании этого конуса, а точка B_{1}
есть ортогональная проекция точки B
, лежащей в плоскости, проходящей через вершину конуса параллельно его основанию. Постройте проекцию (изображение) точки, в которой отрезок AB
пересекает боковую поверхность конуса.
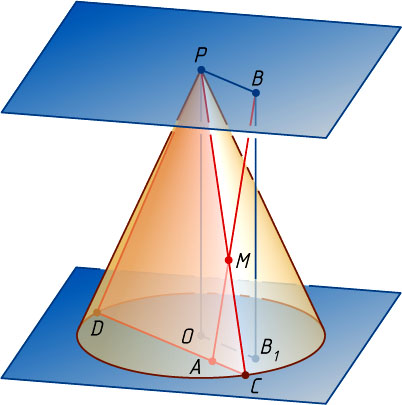
Решение. Пусть P
— вершина конуса, O
— центр основания, точки A
и B_{1}
лежат внутри окружности основания, причём B_{1}
— проекция на основание некоторой точки, лежащей в плоскости, проходящей через точку P
, параллельно основанию конуса (рис. 1). Через точку A
проведём прямую, параллельную OB_{1}
. Пусть проведённая прямая пересекает окружность основания в точках C
и D
. Тогда плоскость CPD
параллельна прямой OB_{1}
, а так как PB\parallel OB_{1}
, то PB\parallel CD
, значит, точка B
лежит в плоскости CPD
. Поэтому прямые PC
, PD
и AB
лежат в одной плоскости. Следовательно, прямая AB
пересекает либо образующую CP
, либо образующую DP
. Отсюда вытекает следующее построение на данном изображении.
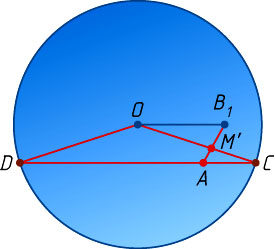
Строим центр O
данной окружности (рис. 2). Через точку A
проводим хорду CD
, параллельную OB_{1}
. Проводим радиусы OC
и OD
. Один из них пересекает отрезок AB_{1}
в искомой точке M
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 12, с. 82

