8345. Высота цилиндра равна h
, радиус основания равен r
. Найдите наибольшее значение площади ортогональной проекции этого цилиндра на плоскость.
Ответ. r\sqrt{4h^{2}+\pi^{2}r^{2}}
.
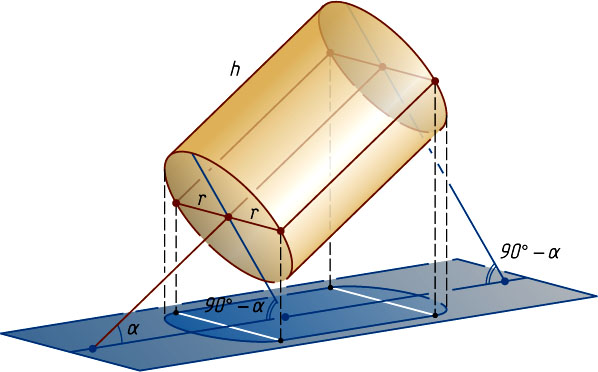
Решение. Заметим, что если ось цилиндра образует с плоскостью проекции угол \alpha
, то плоскости оснований цилиндра образуют с плоскостью проекции угол 90^{\circ}-\alpha
. Пусть S'
— площадь ортогональной проекции цилиндра на некоторую плоскость. Тогда
S'=2rh\cos\alpha+\pi r^{2}\cos(90^{\circ}-\alpha)=2rh\cos\alpha+\pi r^{2}\sin\alpha=
=r(2h\cos\alpha+\pi r\sin\alpha)\leqslant r\sqrt{4h^{2}+\pi^{2}r^{2}},
причём равенство достигается в случае, когда \alpha=\arccos\frac{2h}{\sqrt{4h^{2}+\pi^{2}r^{2}}}
.
Источник: Соросовская олимпиада. — 1997-1998, IV, 2-й тур, 11 класс
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 14, с. 83
