8346. Даны два шара радиусов 2 и 3 с центрами A
и B
соответственно, AB=7
. Плоскость, касающаяся шаров, пересекает прямую AB
в точке M
. Найдите AM
.
Ответ. 14 или \frac{14}{5}
.
Решение. Пусть указанная плоскость касается данных шаров в точках A_{1}
и B_{1}
соответственно. Прямые AA_{1}
и BB_{1}
перпендикулярны этой плоскости, поэтому AA_{1}\parallel BB_{1}
. Рассмотрим сечение шаров плоскостью, проходящей через параллельные прямые AA_{1}
и BB_{1}
. Получим два круга радиусов 2 и 3 с центрами A
и B
соответственно. Прямая A_{1}B_{1}
касается этих кругов соответственно в точках A_{1}
и B_{1}
и пересекает с прямой AB
в точке M
.
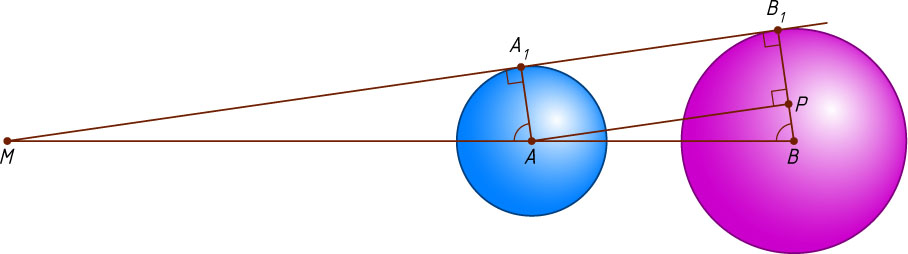
Пусть точка M
лежит вне отрезка AB
(рис. 1). Опустим перпендикуляр AP
из точки A
на прямую BB_{1}
. Из подобия треугольников MAA_{1}
и ABP
следует, что \frac{AM}{AB}=\frac{AA_{1}}{BP}
. Значит,
AM=AB\cdot\frac{AA_{1}}{BP}=AB\cdot\frac{AA_{1}}{BB_{1}-AA_{1}}=7\cdot\frac{2}{1}=14.
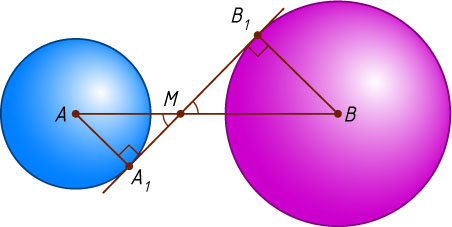
Пусть точка M
лежит на отрезке AB
(рис. 2). Из подобия треугольников MAA_{1}
и MBB_{1}
следует, что
\frac{AM}{BM}=\frac{AA_{1}}{BB_{1}}=\frac{2}{3}.
Значит,
AM=\frac{2}{5}AB=\frac{2}{5}\cdot7=\frac{14}{5}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 1, с. 84

