8347. Осевым сечением конуса является равносторонний треугольник со стороной 4. Шар касается плоскости основания конуса в точке M
и боковой поверхности конуса. Найдите радиус шара, если расстояние от точки M
до оси конуса равно: а) 1; б) 3.
Ответ. а) \frac{1}{\sqrt{3}}
; б) \sqrt{3}
.
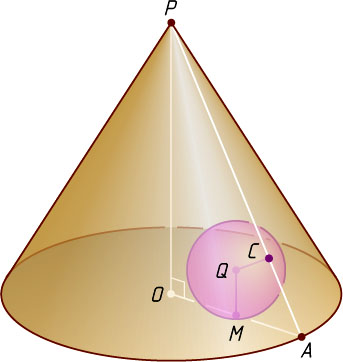
Решение. Пусть P
— вершина конуса, O
— центр основания, Q
— центр шара, C
— точка касания шара с боковой поверхностью цилиндра (рис. 1 и 3). Рассмотрим осевое сечение цилиндра, проходящее через точку Q
.
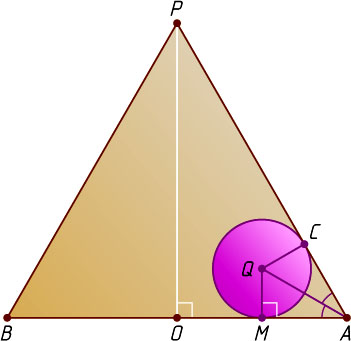
а) Получим равносторонний треугольник APB
(точка M
между O
и A
, OM=1
) и круг, вписанный в угол BAP
(рис. 2). Так как AQ
— биссектриса этого угла, то \angle QAM=30^{\circ}
. Из прямоугольного треугольника QAM
находим, что
QM=AM\tg\angle QAM=(OA-OM)\tg30^{\circ}=(2-1)\cdot\frac{1}{\sqrt{3}}=\frac{1}{\sqrt{3}}.
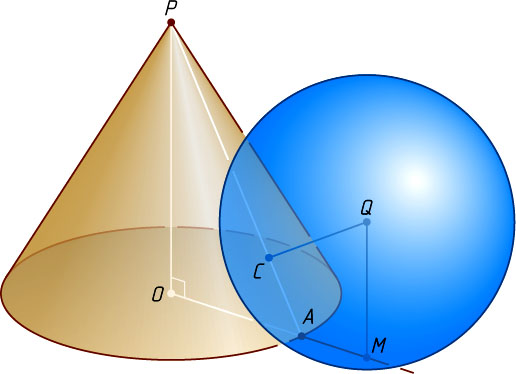
б) Получим равносторонний треугольник APB
(точка M
лежит на продолжении OA
за точку A
и AM=1
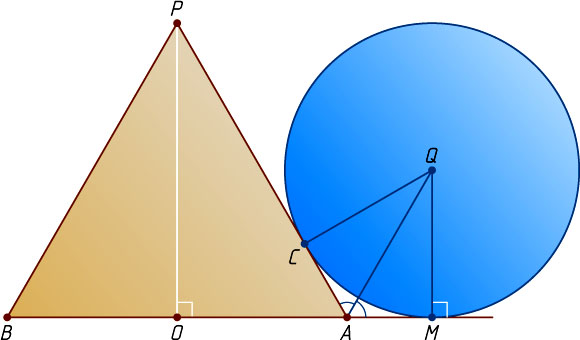
) и круг, вписанный в угол, смежный с углом BAP
(рис. 4). Так как AQ
— биссектриса этого угла, то \angle QAM=60^{\circ}
. Из прямоугольного треугольника QAM
находим, что
QM=AM\tg\angle QAM=AM\tg60^{\circ}=1\cdot\sqrt{3}=\sqrt{3}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 2, с. 84



