8348. Осевым сечением цилиндра является единичный квадрат. Найдите радиус наименьшей сферы, проходящей через центр квадрата и касающейся боковой поверхности цилиндра.
Ответ. \frac{1}{4}
.
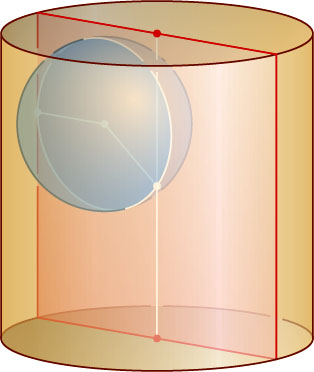
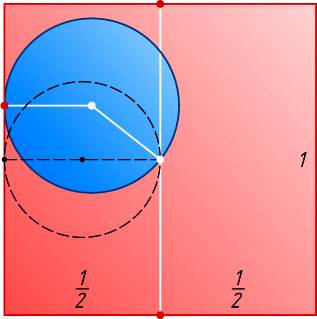
Решение. Рассмотрим произвольную сферу, проходящую через центр квадрата и касающуюся боковой поверхности цилиндра (рис. 1). Проведём плоскость через ось цилиндра и точку касания (рис. 2). Получим единичный квадрат и окружность, проходящую через его центр и касающуюся стороны квадрата (образующей цилиндра), причём центр окружности совпадает с центром сферы. Ясно, что радиус наименьшей из таких окружностей равен \frac{1}{4}
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 3, с. 84

