8349. Даны плоскость \alpha
и перпендикулярная ей прямая l
. Найдите геометрическое место центров шаров радиуса r
, касающихся одновременно плоскости \alpha
и прямой l
.
Ответ. Две окружности радиуса r
, лежащие в плоскостях, параллельных данной, и удалённых от данной на расстояние r
.
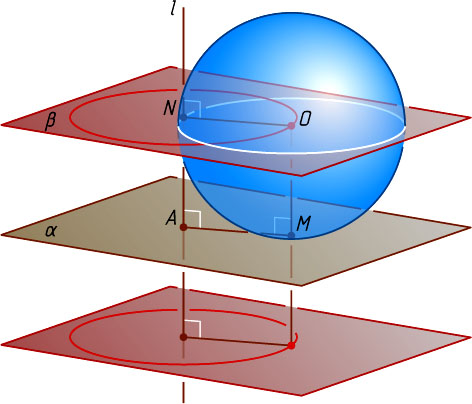
Решение. Пусть O
— центр шара радиуса r
; M
и N
— точки касания шара с плоскостью \alpha
и прямой l
соответственно, A
— точка пересечения прямой l
с плоскостью \alpha
. Так как l\perp\alpha
и OM\perp\alpha
, то OM\parallel AN
. Проведём плоскость через параллельные прямые OM
и AN
. Получим окружность с центром O
радиуса r
, вписанную в прямой угол MAN
. Четырёхугольник OMAN
— квадрат, NO=AM=r
, AN=OM=r
. Поэтому, во-первых, точка O
лежит в плоскости \beta
, параллельной плоскости \alpha
и удалённой от неё на расстояние r
, во-вторых, точка O
удалена от фиксированной точки N
плоскости \beta
, на расстояние r
. Следовательно, точка O
лежит на окружности радиуса r
с центром N
, лежащей в плоскости \beta
. Условию задачи удовлетворяет также окружность, симметричная рассмотренной относительно плоскости \alpha
.
Очевидно, что любая точка каждой из этих окружностей является центром шара радиуса r
, касающегося плоскости \alpha
и прямой l
.
